Question

The line $y = mx$ bisects the area enclosed by the lines $x = 0,\,y = 0$ and $x = \dfrac{3}{2}$ and the curve $y = 1 + 4x - {x^2}$ . Then the value of $m$ is:
A. $\dfrac{{13}}{6}$
B. $\dfrac{{13}}{2}$
C. \[\dfrac{{13}}{5}\]
D. \[\dfrac{{13}}{7}\]

Answer 1

Hint: Since, the line $y = mx$ bisects the area enclosed by the given lines and curves, therefore, equate the area enclosed by the given lines and curves with twice the area enclosed by the line $y = mx$ and the x-axis. Using this expression, find the value of $m$.

Formula Used: Area, \[A = \mathop \smallint \nolimits_a^b \left[ {f(x) - g(x)} \right]\:dx\]

Complete step by step Solution:
Given lines are: $x = 0,\,y = 0$ and $x = \dfrac{3}{2}$
And curve: $y = 1 + 4x - {x^2}$
We know that, if \[f\left( x \right)\] and \[g\left( x \right)\] are continuous on \[\left[ {a,{\text{ }}b} \right]\] and \[g\left( x \right){\text{ }} < {\text{ }}f\left( x \right)\] for all $x$ in \[\left[ {a,{\text{ }}b} \right]\] , then we have the following formula.
Required area, \[A = \mathop \smallint \nolimits_a^b \left[ {f(x) - g(x)} \right]\:dx\]
The line $y = mx$ bisects the area enclosed by the given lines and curves.
Therefore, ${A_2} = 2{A_1}$ ...(1)
Where ${A_1}$ is the area enclosed by the line $y = mx$ and the x-axis, and ${A_2}$ is the area enclosed by the given lines and curves.

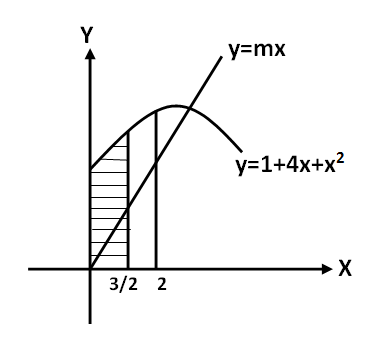
From the diagram above we can see that, ${A_1} = \int_0^{\dfrac{3}{2}} {\left( {mx} \right)dx} $ ...(2)
And ${A_2} = \int_0^{\dfrac{3}{2}} {\left( {y = 1 + 4x - {x^2}} \right)dx} $ ...(3)
Substituting the equations (2) and (3) in equation (1), we get,
 $\int_0^{\dfrac{3}{2}} {\left( {1 + 4x - {x^2}} \right)dx} = 2\int_0^{\dfrac{3}{2}} {\left( {mx} \right)dx} $
 Integrating this, we get, $\left( {\dfrac{3}{2} + 4\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{3}} \right)_0^{\dfrac{3}{2}} = 2m\left( {\dfrac{{{x^2}}}{2}} \right)_0^{\dfrac{3}{2}}$
Putting the limits, we get, $\left( {\dfrac{3}{2} + 4\dfrac{{{{\left( {\dfrac{3}{2}} \right)}^2}}}{2} - \dfrac{{{{\left( {\dfrac{3}{2}} \right)}^3}}}{3}} \right) = 2m\left( {\dfrac{{{{\left( {\dfrac{3}{2}} \right)}^2}}}{2}} \right)$
Solving this, we get, $\dfrac{3}{2} + \dfrac{9}{2} - \dfrac{9}{8} = m\left( {\dfrac{9}{4}} \right)$
Solving further, we get, $\dfrac{{12 + 36 - 9}}{8} = m\left( {\dfrac{9}{4}} \right)$
This implies, $\dfrac{{39}}{8} = m\left( {\dfrac{9}{4}} \right)$
This gives, $m = \left( {\dfrac{{13}}{6}} \right)$

Therefore, the correct option is (A).

Note: To determine the bounds of the area that needs to be calculated, one needs to determine the coordinates of the points where the two curves overlap. The class of problems involving the regions between two curves is the most prevalent when determining the area of bounded regions. Its subset can be thought of as all other situations. These problems not only serve as a significant example of the use of definite integrals, but they also provide insight into the characteristics of the two curves in question.