Question

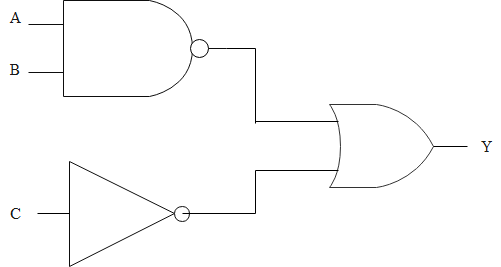
The input to the digital circuit are as shown below: The output Y is:

(A) $A+B+\bar{C}$
(B) $(A+B) \bar{C}$
(C) $\bar{A}+\bar{B}+\bar{C}$
(D) $\bar{A}+\bar{B}+C$

Answer 1

Hint: We know that a Digital Logic Gate is an electronic circuit which makes logical decisions based on the combination of digital signals present on its inputs. Digital logic gates can have more than one input, for example, inputs A, B, C, D etc., but generally only have one digital output, (Q). Digital logic is fundamental in creating electronic devices. It is used to create circuits and logic gates, as well as to check computer chips. Knowledge of digital logic lends itself to many different computer technology design and engineering professions.

Complete step by step answer
We know that logic gates perform basic logical functions and are the fundamental building blocks of digital integrated circuits. Most logic gates take an input of two binary values, and output a single value of a 1 or 0. Some circuits may have only a few logic gates, while others, such as microprocessors, may have millions of them.
We can say that NAND and NOR can be used to build any of the gates i.e. AND, OR, NOT, XOR, XNOR. That is why all the gates are made using these two gates only. not only it reduces cost for building different gates over a chip, it reduces the hardware also. NAND and NOR are preferred because they are smaller and use less power in a CMOS process than equivalent AND or OR gates. NAND and NOR gates can be created with 4 transistors, while AND/OR require 6. An AND/OR gate is laid out in a cell library generally as a NAND/NOR followed by an inverter.
We can say that:
$\mathrm{A}$ and $\mathrm{B}$ are inputs to the NAND gate. The output of that gate is $\overline{(\mathrm{A.B})}=\overline{\mathrm{A}}+\overline{\mathrm{B}}$
The output of $\mathrm{C}$ being input to the NOT gate is $\overline{\mathrm{C}}$. These two are inputs of the OR gate. Hence $\mathrm{Y}=\overline{(\mathrm{A.B})}+\overline{\mathrm{C}}$
$=\overline{\mathrm{A}}+\overline{\mathrm{B}}+\overline{\mathrm{C}}$

Hence the correct answer is option C.

Note: We know that the AND gate is so named because, if 0 is called "false" and 1 is called "true," the gate acts in the same way as the logical "and" operator. The output is "true" when both inputs are "true." Otherwise, the output is "false." In other words, the output is 1 only when both inputs one AND two are 1. When a transistor is on, or open, then an electric current can flow through. When we string a bunch of these transistors together, then we get what's called a logic gate, which lets us add, subtract, multiply, and divide binary numbers in any way imaginable. In a physical circuit, these logic gates have: Inputs.