Question

The free end of a thread wound on a bobbin of inner radius \[r\] and outer radius \[R\] is passed around a nail A hammered into a wall as shown in the figure. The thread is pulled at a constant velocity \[v\]. Find the velocity \[{v_0}\]​ of the bobbin instant when the thread from an angle \[\alpha \] with the vertical, assuming that the bobbin rolls over the horizontal surface without slipping.

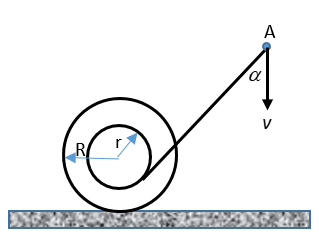
Answer 1

Hint: For pure rolling of the bobbin the point attached to the surface will be at instantaneous rest. When the center of mass is having a linear velocity towards the right then the friction force will try to oppose the motion and act in the backward direction. To make it a pure rolling motion the rotation of the bobbin will be clockwise.

Formula used:
For no slipping condition \[v = r\omega \]
Here v is the linear speed at the point r from the axis of rotation with angular speed \[\omega \].

Complete step by step solution:

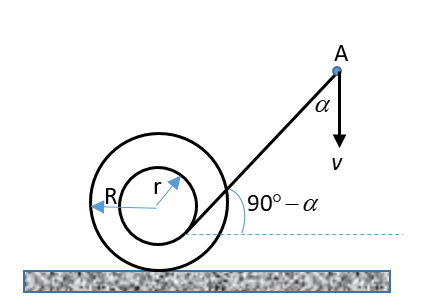
Image: Thread wounded bobbin

Let the bobbin have an angular velocity of \[\omega \] (anti-clockwise) at that instant when the velocity at point A is \[v\]. Assuming the thread to be inextensible, horizontal component of the velocity at the point the thread is attached to the bobbin will be,
\[{v_h} = {v_0}\cos \left( {90^\circ - \alpha } \right) = {v_0}\sin \alpha \]
Vertical component of the velocity at the point the thread is attached to the bobbin will be,
\[{v_v} = {v_0}\sin \left( {90^\circ - \alpha } \right) = {v_0}\cos \alpha \]

For no slipping motion of the bobbin,
\[{v_0} = R\omega \]
At the point of contact,
\[v = r\omega - {v_h}\]
\[\Rightarrow v = r\left( {\dfrac{{{v_0}}}{R}} \right) - {v_0}\cos \alpha \]
\[\Rightarrow v = \left( {\dfrac{r}{R} - \cos \alpha } \right){v_0}\]
\[\Rightarrow {v_0} = \dfrac{v}{{\left( {\dfrac{r}{R} - \cos \alpha } \right)}}\]
Hence, the velocity of the bobbin at the instant when the thread makes angle \[\alpha \]with the vertical can be expressed as \[\dfrac{v}{{\left( {\dfrac{r}{R} - \cos \alpha } \right)}}\].

Therefore, the correct answer is\[\dfrac{v}{{\left( {\dfrac{r}{R} - \cos \alpha } \right)}}\].

Note: When the thread is inextensible then the velocity of every point on the thread is the same. So, the speed at the end where the speed is v will be the same as the end where thread is attached to the bobbin.