Question

The distance between the vertex and the centre of mass of a uniform solid planar circular segment of angular size $\theta$ and radius $R$ is given by:

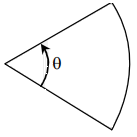
A) $\dfrac{4}{3}R\dfrac{{\sin \dfrac{\theta }{2}}}{\theta }$
B) $R\dfrac{{\sin \dfrac{\theta }{2}}}{\theta }$
C) $\dfrac{4}{3}R\cos \left( {\dfrac{\theta }{2}} \right)$
D) $\dfrac{2}{3}R\cos \theta $

Answer 1

Hint: We will let the distance between the vertex and the center of mass be x and then with the small element dr and half of the angle as it divide the sector in two part where x lies, we will find out the equation to express the x and then integrate from 0 to R for the center of mass.

Complete step by step solution:
Let center of mass be lie at somewhere point C

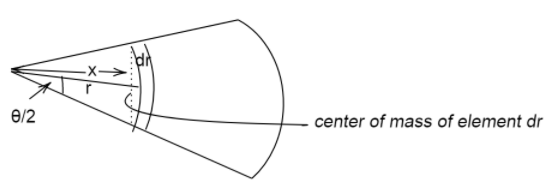
And we need to find the distance of vertex and center of mass say OC
R is the radius in the figure. Let us take a small element $dr$
The mass of the sector is uniform.
Let $\sigma $ (mass density) or mass per unit area
Mathematically to find the arc of the sector we have, arc = $\theta \times r$, where $\theta $ is the angle made by sector and r is the radius.
Then the area of the small element is $r\theta dr$ and by multiplying it with density we will get its mass.
So, for the small arc element dr the mass will be $dm$ = $\sigma r\theta dr$ here dm is the mass along dr.
Let the center of mass lie at point which is x distance far from the vertex.
Then $x$=$\dfrac{{r\sin \dfrac{\theta }{2}}}{{\dfrac{\theta }{2}}}$ , Now to get the center of mass we need to integrate x with the dm
$\Rightarrow {x_{center{\text{ }}of{\text{ }}mass}}$ =$\dfrac{{\int\limits_0^R {xdm} }}{{\int\limits_0^R {dm} }}$ and range will be from 0 to R
Now, putting the values
$\Rightarrow {x_{center{\text{ }}of{\text{ }}mass}}$ =$\dfrac{{\int\limits_0^R {r\sin \dfrac{\theta }{2} \times \sigma \left( {r\theta } \right)dr} }}{{\int\limits_0^R {\sigma \left( {r\theta } \right)dr} }}$
Taking out the constant terms and cancelling out we will get,
$\Rightarrow {x_{center{\text{ }}of{\text{ }}mass}}$ =$\dfrac{{2\sin \dfrac{\theta }{2}\int\limits_0^R {{r^2}dr} }}{{\theta \int\limits_0^R {rdr} }}$
Taking the limits from 0 to R, this is now equal to after integrating is,
$\Rightarrow \dfrac{{2\sin \dfrac{\theta }{2}R}}{\theta } \times \dfrac{{\dfrac{{{R^3}}}{3}}}{{\dfrac{{{R^2}}}{2}}}$
On further solving we can write it as $\dfrac{{4R\sin \dfrac{\theta }{2}}}{{3\theta }}$.
So, ${x_{center{\text{ }}of{\text{ }}mass}}$ = $\dfrac{{4R\sin \dfrac{\theta }{2}}}{{3\theta }}$(from vertex)

Hence option A is correct.

Additional information:
Center of mass: The center of mass is a position defined relative to an object or system of objects. It is the average position of all the parts of the system, weighted according to their masses. For simple rigid objects with uniform density, the center of mass is located at the centroid.
A circle is a 2D object as stated above but when we talk about the 3D object then a circle is known as a sphere and has a different formula for the area and volume
Area of sphere =$4\pi {r^2}$
And volume of sphere =$\dfrac{4}{3}\pi {r^3}$ where r is the radius
There are some important points regarding the circle which might be asked in different question
Sector of a circle
A circle can be divided into many parts as a sector as shown in fig.

Chord of a circle
A chord divides a circle in two parts. It may or may not divide in equal parts as shown in the diagram.

Note: There are many points where mistakes can happen; the only simple rule of integration needs to be remembering that in numerator function power plus one and denominator is power plus one. Taking out of the constant terms and cancelling out is important to be done cautiously.