Question

The area of the region formed by ${x^2} + {y^2} - 6x - 4y + 12 \leqslant 0$, $y \leqslant x$, and $x \leqslant \dfrac{5}{2}$ is
A. $\left( {\dfrac{\pi }{6} - \dfrac{{\sqrt 3 + 1}}{8}} \right)$ sq. unit
B. $\left( {\dfrac{\pi }{6} + \dfrac{{\sqrt 3 - 1}}{8}} \right)$ sq. unit
C. $\left( {\dfrac{\pi }{6} - \dfrac{{\sqrt 3 - 1}}{8}} \right)$ sq. unit
D. None of these

Answer 1

Hint: In this question, we are given the equation of circle and the lines. By adding $9$ and $4$both the sides covert the equation as general equation of the circle to know the coordinate of centre. Then, plot the graph of the required coordinate and the given equation. In last calculate the area by the integrating of the difference of equation $y = x$ and $y = 2 - \sqrt {1 - {{\left( {x - 3} \right)}^2}} $ (given equation of the circle) with respect to $dx$ from $x = 2$ to $x = \dfrac{5}{2}$. Then, solve it further using integration formulas.



Formula Used:Algebraic identity –
${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$
General equation of circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = a$ where $\left( {h,k} \right)$ is the centre and $a$ is radius
Integration formula –
$\int {cdx = cx} $ where $c$ is the constant
$\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $
$\int {\dfrac{1}{{\sqrt {1 - {x^2}} }}} dx = {\sin ^{ - 1}}x + c$



Complete step by step solution:Given that,
Equation of the circle ${x^2} + {y^2} - 6x - 4y + 12 \leqslant 0$
Also, written as ${x^2} + {y^2} - 6x - 4y \leqslant - 12$
Add $9$ and $4$both the sides, we get
${x^2} + 9 - 6x + {y^2} + 4 - 4y \leqslant - 12 + 9 + 4$
It implies that, ${x^2} + {\left( 3 \right)^2} - 6x + {y^2} + {\left( 2 \right)^2} - 4y \leqslant - 1$
Using the algebraic identity ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$
We get, ${\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} \leqslant - 1$
Also written as, ${\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} \geqslant 1$
Compare the above equation with the general equation of circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = a$ where $\left( {h,k} \right)$ is the centre and $a$ is radius.
It implies that, $\left( {3,2} \right)$ is the centre and $1$ unit is the radius of the given circle.
Graph of the given equations and the required coordinate is attached below (figure 1);


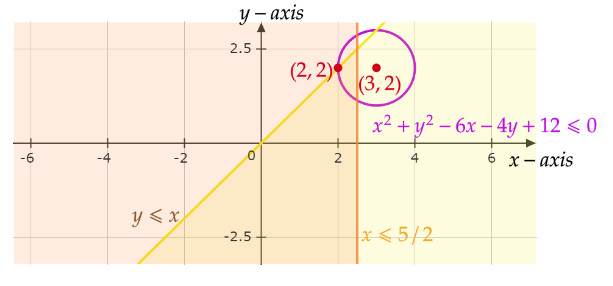
Figure 1: A Graph contains the plot of the given circle and the lines with the shaded bounded region
Therefore, the area of the bounded region will be the integration of the difference of equation $y = x$ and $y = 2 - \sqrt {1 - {{\left( {x - 3} \right)}^2}} $ (given equation of the circle) with respect to $dx$ from $x = 2$ to $x = \dfrac{5}{2}$.
Thus, the area of the required region will be
$A = \int\limits_2^{\dfrac{5}{2}} {xdx} - \int\limits_2^{\dfrac{5}{2}} {\left[ {2 - \sqrt {1 - {{\left( {x - 3} \right)}^2}} } \right]dx} $
As we know that, $\int {cdx = cx} $ where $c$ is the constant and $\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $
$A = \left[ {\dfrac{{{x^2}}}{2}} \right]_2^{\dfrac{5}{2}} - \left[ {2x} \right]_2^{\dfrac{5}{2}} - \int\limits_2^{\dfrac{5}{2}} {\left[ {2 - \sqrt {1 - {{\left( {x - 3} \right)}^2}} } \right]dx} $
Now, using $\int {\dfrac{1}{{\sqrt {1 - {x^2}} }}} dx = {\sin ^{ - 1}}x + c$
$ = \left[ {\dfrac{{{x^2}}}{2}} \right]_2^{\dfrac{5}{2}} - \left[ {2x} \right]_2^{\dfrac{5}{2}} + \left[ {\dfrac{{x - 3}}{2}\sqrt {1 - {{\left( {x - 3} \right)}^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\left( {x - 3} \right)} \right]_2^{\dfrac{5}{2}}$
On resolving limits, we get
$ = \left[ {\dfrac{{{{\left( {\dfrac{5}{2}} \right)}^2}}}{2} - \dfrac{{{{\left( 2 \right)}^2}}}{2}} \right] - \left[ {2\left( {\dfrac{5}{2}} \right) - 2\left( 2 \right)} \right] + \left[ {\dfrac{{\left( {\dfrac{5}{2}} \right) - 3}}{2}\sqrt {1 - {{\left( {\left( {\dfrac{5}{2}} \right) - 3} \right)}^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\left( {\left( {\dfrac{5}{2}} \right) - 3} \right) - \left( {\dfrac{{2 - 3}}{2}\sqrt {1 - {{\left( {2 - 3} \right)}^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\left( {2 - 3} \right)} \right)} \right]$
On solving, we get
$ = \dfrac{9}{8} - 1 + \left( { - \dfrac{{\sqrt 3 }}{8} + \dfrac{\pi }{6}} \right)$
$ = \dfrac{\pi }{6} - \dfrac{{\sqrt 3 - 1}}{8}$ sq. unit



Option ‘C’ is correct

Note: Different methods are used to determine the area under the curve, with the antiderivative method being the most prevalent. The area under the curve can be calculated by knowing the curve's equation, borders, and the axis surrounding the curve. There exist formulas for obtaining the areas of regular shapes such as squares, rectangles, quadrilaterals, polygons, and circles, but no formula for finding the area under a curve. The integration procedure aids in solving the equation and determining the required area. Antiderivative methods are highly useful for determining the areas of irregular planar surfaces.