Question

The area enclosed between the curves \[y = lo{g_e}(x + e)\], \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\] and the x-axis is
A) $2$ sq. units
B) $1$ sq. units
C) $4$ sq. units
D) None of these

Answer 1

Hint: In this we are given the equation of two curves. Firstly, convert the second curve in the form of $x$ because we need to find the area till $x - axis$. Now, using the first curve calculate the coordinate on $x - axis$ by taking $y = 0$. Calculate the area by the integration of the required equation of the curve and solve it further by applying the ILATE rule.

Formula Used: ILATE Rule of integration
Here, the full form of ILATE is Inverse, Logarithms, Algebraic, Trigonometric, and Exponential. We use this series to select which of the first will be $\left( {u\left( x \right)} \right)$ or $\left( {v\left( x \right)} \right)$. Here, the first function will be the function that comes first in this series.
$\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
Lorartithm formula –
$\log 1 = 0$
$\log e = 0.43429$
${a^x} = y \Leftrightarrow {\log _a}y = x$

Complete step by step Solution:
We are given two equations of curve \[y = lo{g_e}(x + e)\] and \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
We have \[x = lo{g_e}\left( {\dfrac{1}{y}} \right)\;\]
Also written as,
$x = {\log _e}1 - {\log _e}y$
$x = - {\log _e}y$
${\log _a}y = - x$
$y = {e^{ - x}}$
For \[y = lo{g_e}(x + e)\], we’ll shift the graph of the curve $y = {\log _e}x$, $e$ units at the left-hand side because at $y = 0$ the value of $x = 1 - e$
Let’s mark all the curves in the graph, Graph is attached below;

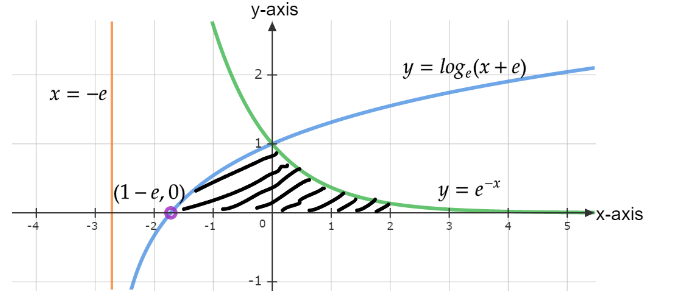
Figure 1: A Graph of given curves with the point (1-e,0)
Now, the area of the shaded region will be
$A = \int\limits_{1 - e}^0 {1 \times {{\log }_e}\left( {x + e} \right)dx} + \int\limits_0^\infty {{e^{ - x}}dx} $
Applying ILATE rule, i.e., $\int {u(x)v\left( x \right)dx = u\left( x \right)\int {v\left( x \right)dx} - \int {\left( {\dfrac{{du\left( x \right)}}{{dx}}\int {v\left( x \right)dx} } \right)} dx} $
$ = \left[ {x{{\log }_e}\left( {x + e} \right)} \right]_{1 - e}^0 - \int\limits_{1 - e}^0 {\dfrac{x}{{x + e}}dx} - \left[ {{e^{ - x}}} \right]_0^\infty $
$ = \left[ {\left( 0 \right){{\log }_e}\left( {0 + e} \right) - \left( {1 - e} \right){{\log }_e}\left( {1 - e + e} \right)} \right] - \int\limits_{1 - e}^0 {\dfrac{{x + e - e}}{{x + e}}dx} - \left( {{e^{ - \infty }} - {e^0}} \right)$
As we know, $\log 1 = 0$
$ = 0 - \int\limits_{1 - e}^0 {1 - \dfrac{e}{{x + e}}dx} - \left( {0 - 1} \right)$
$ = - \left[ {x - e\log \left( {x + e} \right)} \right]_{1 - e}^0 + 1$
$ = - \left[ {0 - e\log \left( {0 + e} \right) - \left( {1 - e} \right) + e\log \left( {1 - e + e} \right)} \right] + 1$
$ = - \left[ { - e - 1 + e + e\left( 0 \right)} \right] + 1$
$ = 2$ sq. Units

Therefore, the correct option is (A).

Note: To solve such a question, one should have a good knowledge of logarithm and integration formulas. Also, if you are changing the function and then always change the limits too. Put the limits in the same to calculate new limits. Try to open terms using trigonometric identities as much as it is possible. And to solve the limits, firstly solve the integration past then last subtract the terms (put the upper limit values and then lower limits).