Question

Take the z=axis as vertical and the x-y plane as horizontal. A particle ‘A’ is projected with velocity $4\sqrt 2 m{s^{ - 1}}$ making an angle $45^\circ $ to the horizontal. Particle B is projected at $5m{s^{ - 1}}$ an angle $\theta = {\tan ^{ - 1}}\left( {\dfrac{1}{3}} \right)$ to y axis in y-z plane then velocity of B wrt A.
A) Has its initial magnitude$5m{s^{ - 1}}$.
B) Magnitude will change with time.
C) Lies in the xy plane.
D) Will initially make an angle$\left( {\theta + \dfrac{\pi }{2}} \right)$.

Answer 1

Hint: The x,y and z are the three directions which are mutually perpendicular to each other, the particle A is in plane x-z and the particle B is in the plane y-z. The relative velocity is the difference between the velocities of the two bodies.

Formula used:
The relative velocity of the two particles is given by,
$ \Rightarrow {v_B} - {v_A}$
Where the velocity of particle B is ${v_B}$ and the velocity of particle A is${v_A}$.

Complete step by step solution:
In this problem it is given that a particle ‘A’ is projected with velocity $4\sqrt 2 m{s^{ - 1}}$ making an angle $45^\circ $ to the horizontal. Particle B is projected at $5m{s^{ - 1}}$ an angle $\theta = {\tan ^{ - 1}}\left( {\dfrac{1}{3}} \right)$ to y axis in y-z plane then we need to find the velocity of B wrt A.
According to the condition the figure will be.

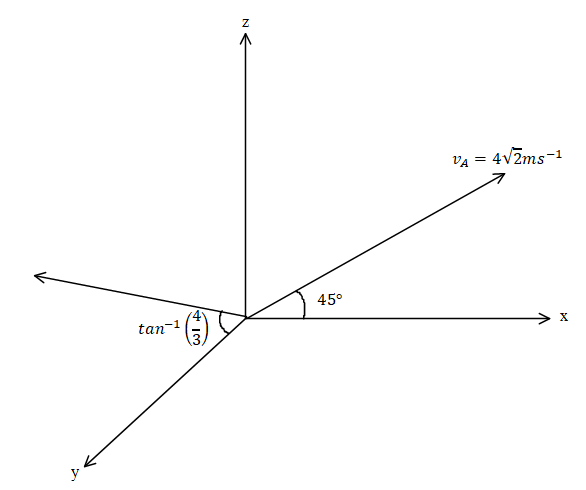
The velocity of particle A is ${v_A} = 4\hat i + 4\hat k$ and the velocity of particle B is equal to ${v_B} = 3\hat j + 4\hat k$.
The relative velocity of the particle B with respect to particle A is equal to,
$ \Rightarrow {v_B} - {v_A} = \left( {3\hat j + 4\hat k} \right) - \left( {4\hat i + 4\hat k} \right)$
$ \Rightarrow {v_B} - {v_A} = 3\hat j + 4\hat k - 4\hat i - 4\hat k$
$ \Rightarrow {v_B} - {v_A} = 3\hat j + 4\hat k - 4\hat i - 4\hat k$
$ \Rightarrow {v_B} - {v_A} = 3\hat j - 4\hat i$
The magnitude of the velocity is equal to,
$ \Rightarrow {v_B} - {v_A} = \sqrt {{3^2} + {4^2}} $
$ \Rightarrow {v_B} - {v_A} = \sqrt {9 + 16} $
$ \Rightarrow {v_B} - {v_A} = \sqrt {25} $
$ \Rightarrow {v_B} - {v_A} = 5m{s^{ - 1}}$
Which means option A is correct. The magnitude of the acceleration will not change with time and therefore the option B is wrong.
The relative velocity is ${v_B} - {v_A} = 3\hat j - 4\hat i$ which means it is in the x-y plane, the option C is also correct. The angle of the initially equal to,
$ \Rightarrow \theta = {\tan ^{ - 1}}\left( { - \dfrac{4}{3}} \right)$
As the angle is negative and therefore we add $\dfrac{\pi }{2}$ so the angle becomes $\theta + \dfrac{\pi }{2}$, so the option D is correct.

The wrong option is option B, so the answer for this problem is option B.

Note: The students are advised to remember the formula of the relative velocity and also the diagram of the velocity of the particle A and particle B should be drawn very carefully as the answer is very dependent on the diagram.