Question

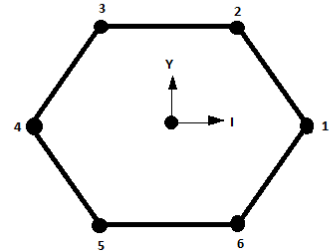
Six objects are placed at the vertices of a regular hexagon. The geometric center of the hexagon is at the origin with objects \[1\] and \[4\] on the x-axis (see figure). The mass of the \[{k^{th}}\]object is \[{m_k} = {k^i}M\left| {cos{\theta _k}} \right|\]where \[i\] is an integer, M is a constant with dimension of mass, and \[{\theta _k}\] is the angular position of the \[{k^{th}}\] vertex measured from the positive x-axis in the counterclockwise sense. If the net gravitational force on a body at the centroid vanishes, the value of \[i\] is?

$\left( {{A}} \right){{ 0}}$
$\left( {{B}} \right){{ }}1$
$\left( {{C}} \right){{ 2}}$
$\left( {{D}} \right){{ }}3$

Answer 1

Hint: Here, net gravitational force is zero then the forces from the opposite side of the object cancel out.
According to the question we have ,
net gravitational force is equal to zero.
mass of \[{k^{th}}\]object is \[{m_k} = {k^i}M\left| {cos{\theta _k}} \right|\]

Complete step by step answer:
When the net gravitational force is zero then the diagonal opposite vertices of the hexagon should be equal to each other. So, depending upon this theory we will have \[3\] conditions.
\[{m_1} = {{ }}{m_4},{{ }}{m_2} = {{ }}{m_5},{{ }}{m_3} = {{ }}{m_6}\]
We can take any one condition to get the value of I.
Let us take \[{m_1} = {{ }}{m_4}\]
\[{{{k}}^{{i}}}{{M}}\mid {{cos}}{{{\theta }}_{{k}}}{\mid _{{{k = 1}}}} = {{{k}}^{{i}}}{{M}}\mid {{cos}}{{{\theta }}_{{k}}}{\mid _{{{k = 4}}}}\]
The value of \[{{{\theta }}_{{1}}} = 0\] and value of \[{{{\theta }}_2} = 180\]
By substituting we have,
\[\Rightarrow {1^{{i}}}|\cos {{{\theta }}_1}| = {4^{{i}}}|\cos {{{\theta }}_4}|\].
\[\Rightarrow {1^{{i}}}\cos {0^ \circ } = {4^{{i}}}\cos {180^ \circ }\]
Here, \[\cos {0^ \circ } = \cos {180^ \circ } = 1\]
So we can write it as, we get,
\[\Rightarrow {1^{{i}}} = {4^{{i}}}\]
Here \[{1^{{i}}} = 1\]we get,
\[ \Rightarrow 1 = {4^{{i}}}\]
We get,
\[ \Rightarrow {{i = 0}}\]

Hence the correct option is $\left( {{A}} \right)$.

Note: We can get the same value for i if we even consider another two conditions. We can do another method for the same question which gives the same value for\[i\].
Net gravitational force is equal to zero.
All Diagonal opposite vertices should have equal mass.
\[{2^i}M{{ }}cos{{ }}60^\circ = {4^i}M{{ }}cos\left( {60^\circ + 180^\circ } \right)\;\]
So,\[\;I = 0\].