
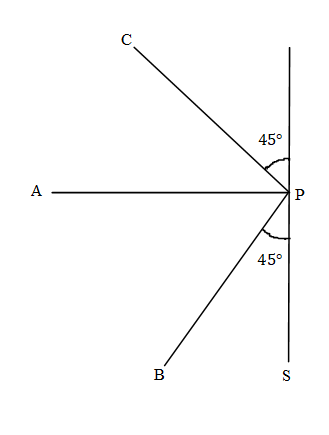
Screen S is illuminated by two point sources A and B. Another source C sends a parallel beam of light towards points P on the screen. Line AP is normal to the screen and the lines AP, BP and CP are 6,3 and 3m respectively. The radiant powers of sources A and B are 45 and 90W respectively. The beam from C is of intensity $0.4\dfrac{{\text{W}}}{{{m^2}}}$. The total incident intensity at P is:
Answer
216.6k+ views
Hint: The intensity is defined as the power transferred per unit area. Power is the energy of the striking light. If intensity is more than it means that the power of the striking light is more and the area at which it is striking is less.
Formula used:
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
Complete step by step solution:
It is given in the problem that Screen S is illuminated by two point sources A and B another source C sends a parallel beam of light towards points P on the screen line AP is normal to the screen and the lines AP, BP and CP are 6,3 and 3m respectively. The radiant powers of sources A and B are 45 and 90W respectively the beam from C is of intensity $0.4\dfrac{{\text{W}}}{{{m^2}}}$ and we need to know the total incident intensity at P.
The total intensity at screen is equal to,
$ \Rightarrow I = {I_A} + {I_B} + {I_C}$
The light from point A is striking at angle $\theta = 0^\circ $.
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The power from point A is 45W and AP is equal to 6m.
The intensity ${I_A}$ is equal to,
$ \Rightarrow {I_A} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$ \Rightarrow {I_A} = \dfrac{{45 \times \cos 0}}{{4\pi \times {6^2}}}$
$ \Rightarrow {I_A} = \dfrac{{45 \times 1}}{{4\pi \times 36}}$
$ \Rightarrow {I_A} = 0.0995\dfrac{{\text{W}}}{{{m^2}}}$
The intensity from source B,
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The angle at which the light strikes the screen is$\theta = 45^\circ $, the power is equal to 90W and r=3m.
$ \Rightarrow {I_B} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$ \Rightarrow {I_B} = \dfrac{{90 \times \cos 45^\circ }}{{4\pi \times {3^2}}}$
$ \Rightarrow {I_B} = \dfrac{{90 \times \dfrac{1}{{\sqrt 2 }}}}{{4\pi \times 9}}$
$ \Rightarrow {I_B} = 0.563\dfrac{{\text{W}}}{{{m^2}}}$
The intensity for the source is equal to,
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The intensity of source at point C is equal to$0.4\dfrac{{\text{W}}}{{{m^2}}}$.
$ \Rightarrow {I_C} = 0.4\dfrac{{\text{W}}}{{{m^2}}}$.
The total intensity is equal to$I$.
$ \Rightarrow I = {I_A} + {I_B} + {I_C}$
$ \Rightarrow I = 0.0995 + 0.563 + 0.4$
$ \Rightarrow I = 1.0625\dfrac{{\text{W}}}{{{m^2}}}$
The total intensity on the screen is equal $1.0625\dfrac{{\text{W}}}{{{m^2}}}$.
Note: The students are advised to remember the formula of the intensity as it is very useful in solving the problems like these. The intensity of the light is proportional to the cosine of angle of incident on the screen.
Formula used:
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
Complete step by step solution:
It is given in the problem that Screen S is illuminated by two point sources A and B another source C sends a parallel beam of light towards points P on the screen line AP is normal to the screen and the lines AP, BP and CP are 6,3 and 3m respectively. The radiant powers of sources A and B are 45 and 90W respectively the beam from C is of intensity $0.4\dfrac{{\text{W}}}{{{m^2}}}$ and we need to know the total incident intensity at P.
The total intensity at screen is equal to,
$ \Rightarrow I = {I_A} + {I_B} + {I_C}$
The light from point A is striking at angle $\theta = 0^\circ $.
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The power from point A is 45W and AP is equal to 6m.
The intensity ${I_A}$ is equal to,
$ \Rightarrow {I_A} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$ \Rightarrow {I_A} = \dfrac{{45 \times \cos 0}}{{4\pi \times {6^2}}}$
$ \Rightarrow {I_A} = \dfrac{{45 \times 1}}{{4\pi \times 36}}$
$ \Rightarrow {I_A} = 0.0995\dfrac{{\text{W}}}{{{m^2}}}$
The intensity from source B,
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The angle at which the light strikes the screen is$\theta = 45^\circ $, the power is equal to 90W and r=3m.
$ \Rightarrow {I_B} = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
$ \Rightarrow {I_B} = \dfrac{{90 \times \cos 45^\circ }}{{4\pi \times {3^2}}}$
$ \Rightarrow {I_B} = \dfrac{{90 \times \dfrac{1}{{\sqrt 2 }}}}{{4\pi \times 9}}$
$ \Rightarrow {I_B} = 0.563\dfrac{{\text{W}}}{{{m^2}}}$
The intensity for the source is equal to,
The formula of the intensity is equal to,
$ \Rightarrow I = \dfrac{{P \times \cos \theta }}{{4\pi {r^2}}}$
Where power is P, radius is r and $\theta $ is the angle at which the light is striking on the screen.
The intensity of source at point C is equal to$0.4\dfrac{{\text{W}}}{{{m^2}}}$.
$ \Rightarrow {I_C} = 0.4\dfrac{{\text{W}}}{{{m^2}}}$.
The total intensity is equal to$I$.
$ \Rightarrow I = {I_A} + {I_B} + {I_C}$
$ \Rightarrow I = 0.0995 + 0.563 + 0.4$
$ \Rightarrow I = 1.0625\dfrac{{\text{W}}}{{{m^2}}}$
The total intensity on the screen is equal $1.0625\dfrac{{\text{W}}}{{{m^2}}}$.
Note: The students are advised to remember the formula of the intensity as it is very useful in solving the problems like these. The intensity of the light is proportional to the cosine of angle of incident on the screen.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Atomic Structure: Definition, Models, and Examples

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




