Question

What is the RMS voltage?
A. \[\sqrt 2 \Delta {V_{\max }}\]
B. \[\Delta {V_{\max }}\]
C. \[\dfrac{{\Delta {V_{\max }}}}{{\sqrt 2 }}\]
D. \[\dfrac{{\Delta {V_{\max }}}}{2}\]
E. \[\dfrac{{\Delta {V_{\max }}}}{4}\]

Answer 1

Hint: In this question, we need to find the root mean square value of the voltage where RMS value is the effective value of the varying voltage and the current. RMS values are mathematical quantities used to compare both the alternating and the direct voltages or current. From the given five options we will find the correct value of RMS voltage.

Complete step by step solution:
In this question we need to write the value of the RMS voltage from the given options.
Root mean square is defined as the value of steady potential difference which generates the same amount of heat for a given resistance in a given time period as the AC voltage when maintained across the same resistance for the same amount of time. RMS is also a way of expressing an AC quantity of voltage and current functionally equivalent to DC.

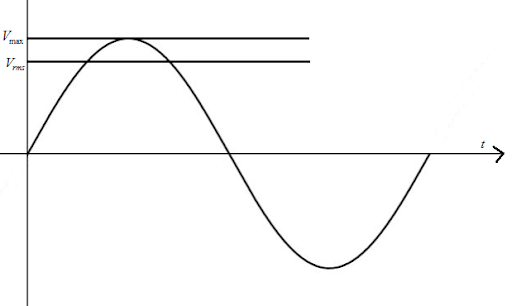
Image: sinusoidal curve of alternating voltage.

The above figure shows the waveform of the Alternating voltage, where \[{V_{RMS}}\] is the RMS voltage and \[{V_{pk}}\] is the peak voltage. RMS voltage of a sinusoidal waveform is calculated by multiplying the peak voltage by \[0.7071\] or the peak voltage is divided by \[\sqrt 2 \], which is represented as,
\[{V_{RMS}} = \dfrac{1}{{\sqrt 2 }}{V_{pk}}\]
Where \[{V_{pk}}\] is the peak voltage

Therefore option C is the correct answer

Note:We know that in case of the Alternating current its average value is always equal to Zero because of the sinusoidal nature of the waveform, hence to measure the effective value of this quantity we use the RMS (root mean square) value.