Question

What is the relation between $Q$ and $q$ for which the potential at center of the square is zero. It is given that, four – point charges $ - Q, - q,2q$ and $2Q$ are placed one at each corner of the square.
(A) $Q = q$
(B) $Q = \dfrac{1}{q}$
(C) $Q = - q$
(D) $Q = - \dfrac{1}{q}$

Answer 1

Hint: Construct the square illustrating the four charges at each corner. Now, use the formula of potential difference for each charge and add them with each other and make them equal to zero.
Formula used The potential difference of the system for a point charge can be calculated by the formula –
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{r}$
where, $Q$ is the charge, and
$r$ is the distance of point

Complete Step by Step Solution
According to the question, it is given that, there are four – point charges $ - Q, - q,2q$ and $2Q$ which are placed at each corner of the square. So, this can be illustrated in the figure as below –

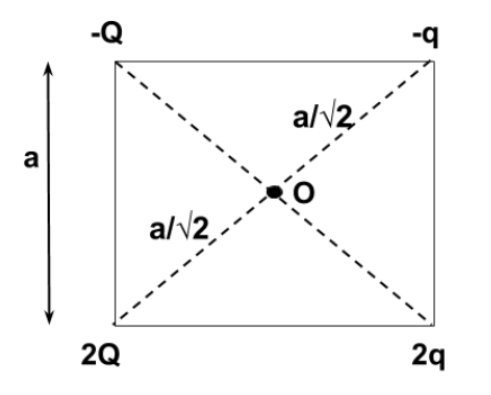
Let the side of the square be $a$ then, the length of each corner from the center will be $\dfrac{a}{{\sqrt 2 }}$.
Now, we know that, the potential difference of the system can be given by the formula –
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{r}$
As, $\dfrac{1}{{4\pi {\varepsilon _0}}}$ is constant. So, let $\dfrac{1}{{4\pi {\varepsilon _0}}}$ be $K$
Hence, -
$ \Rightarrow V = \dfrac{{KQ}}{r}$
Now, the potential at the centre of square from each charge can be given by –
$V = \dfrac{{K\left( { - Q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( { - q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( {2q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( {2Q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}}$
As it is given in question that potential at centre of square is equal to zero. So, $V = 0$
$
  \therefore \dfrac{{K\left( { - Q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( { - q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( {2q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} + \dfrac{{K\left( {2Q} \right)}}{{\dfrac{a}{{\sqrt 2 }}}} = 0 \\
   \Rightarrow - KQ - Kq + 2Kq + 2Kq = 0 \\
   \Rightarrow Kq + KQ = 0 \\
  \therefore Q = - q \\
 $
Now, we got the relation between the charges $Q$ and $q$ as $Q = - q$.

Hence, the correct option is (C).

Note: Potential difference between two points is the work done in moving a unit positive charge between the two points. Its S.I unit is V.
The diagonal of the square can be calculated by multiplying the side of the square with $\sqrt 2 $. So, the length of each corner from the centre of square will be –
$
   \Rightarrow \dfrac{{a\sqrt 2 }}{2} \\
  \therefore \dfrac{a}{{\sqrt 2 }} \\
 $
$\dfrac{a}{{\sqrt 2 }}$ is equal to the half of the diagonal of the square.