Question

Radius of the curved road on the national highway is $R$. Width of the road is $b$. The outer edge of the road is raised by $h$ with respect to the inner edge so that a car with velocity $v$ can pass safely over it. The value of $h$ is
(A) $\dfrac{{{v^2}b}}{{Rg}}$
(B) $\dfrac{v}{{Rgb}}$
(C) $\dfrac{{{v^2}R}}{{bg}}$
(D) $\dfrac{{{v^2}b}}{R}$

Answer 1

Hint: In this question we must apply the concept of equilibrium of the moving bodies. A body will be in equilibrium if all the forces acting on that body or object are balanced. In this question the centripetal force and the contact forces are to balance.

Complete step by step answer:
In this question, we have given the radius of the curved road is $R$, the width of the road is $b$, the outer edge of the road is raised by $h$ with respect to the inner edge, and the velocity of the car is $v$. We need to calculate the value of $h$.

First, we will draw the diagram based on the situation given in the question is shown below,

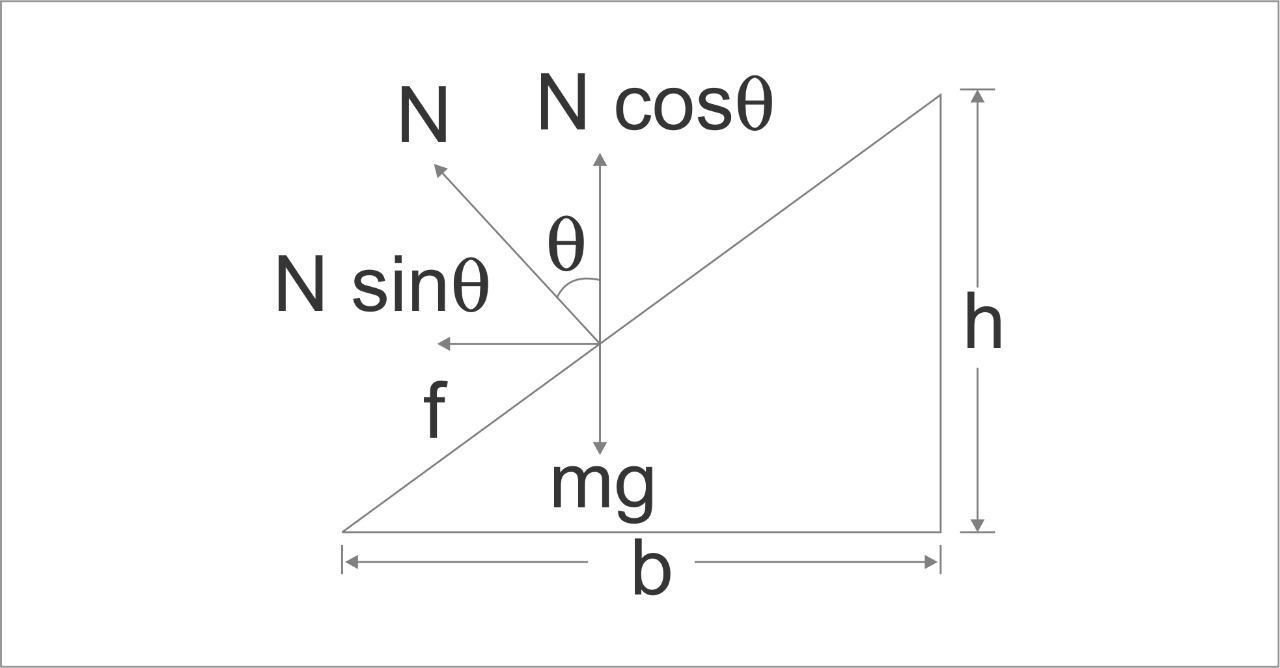
Figure-(1)

In the above diagram, $N$ represents the normal reaction of the car and the slope angle is $\theta $.

Now, we apply the concept of equilibrium for horizontal forces as well as the vertical forces.
From the above diagram, the horizontal forces can be balanced as,
$ \Rightarrow N\sin \theta = \dfrac{{m{v^2}}}{R}......\left( 1 \right)$
Here, $N$ is the normal force, $R$ is the radius of the road, $v$ is the velocity, $m$ is the mass of the vehicle and $\theta $ is the angle between the elevations of the road from the horizontal.
Similarly, the vertical forces can be balanced as,
$ \Rightarrow N\cos \theta = mg......\left( 2 \right)$
Now we divide equation (1) by equation (2) as,
$ \Rightarrow \dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{R}}}{{mg}}$
Further, we solve the above equation.
$ \Rightarrow \tan \theta = \dfrac{{{v^2}}}{{Rg}}......\left( 3 \right)$
Now we calculate $\tan \theta $ from the diagram.
$ \Rightarrow \tan \theta = \dfrac{h}{b}......\left( 4 \right)$
Here, $h$ is the height of the road and $b$ is the width of road.
Now we compare equation (3) and (4) as,
$ \Rightarrow \dfrac{h}{b} = \dfrac{{{v^2}}}{{Rg}}$
After simplification we get,
$\therefore h = \dfrac{{{v^2}b}}{{Rg}}$
Therefore, the correct option is A.

Note: In this question, diagram plays an important role in the calculation. So, the diagrams should be made carefully. While balancing the forces it is necessary to look at the sign of forces because difference in sign will lead to wrong answers.