Question

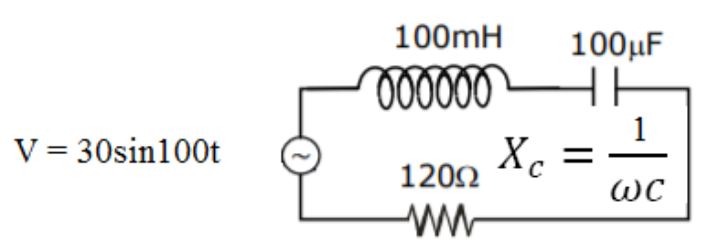
Question: Find the peak current and resonant frequency of the following circuit (as shown in figure).

a. $0.2$A and $100$ Hz.
b. $2$A and $50$ Hz.
c. $2$A and $100$ Hz.
d. $0.2$A and $50$ Hz.

Answer 1

Hint: We have the knowledge or we know the formula regarding the voltage in a LCR circuit. With the help of this formula we will derive out the variables first. Then, we will use the relation between impedance and peak current to find the current in the circuit. Lastly, we will use the relation between frequency to inductance and capacitance to find the resonant frequency of the LCR circuit.

Complete answer:
First of all, the relation between sinusoidal voltage, amplitude, frequency and time is represented as:
$V={{V}_{0}}\sin \omega t$---(i)
Where $V=$ final or sinusoidal voltage
${{V}_{0}}=$ amplitude of the voltage
$\omega =$ frequency of the wave
$t=$ time

The question has already provided us with the relation of sinusoidal voltage as,
$V=30\sin 100t$---(ii)

Therefore, comparing equation (i) and equation (ii) we get,
${{V}_{0}}=30$--(iii) and $\omega =100$---(iv)

Now, the relation between peak current and impedance is given as,
$i=\dfrac{{{V}_{0}}}{Z}$---(v)
Where $i=$ peak current and $Z=$ impedance.

The formula for impedance is,
$Z=\sqrt{{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}+{{R}^{2}}}$---(vi)
The variables are defined as,
${{X}_{L}}$ is the resistance due to inductor, ${{X}_{C}}$ is the resistance due to capacitor and $R$ is the resistance of the circuit.
Again, ${{X}_{L}}=\omega L$---(vii)
$L=$ inductance of the circuit.

Substituting the values given in the question we get,
${{X}_{L}}=100\times (100\times {{10}^{-3}})=10$--(viii)
Now, ${{X}_{C}}=\dfrac{1}{\omega \times C}$--(ix)
Where $C=$ capacitance of the circuit

Substituting the values from the given question we get,
${{X}_{C}}=\dfrac{1}{100\times 100\times {{10}^{-6}}}=100$---(x)

Substituting these values from equation (viii) and (x) to equation (vi) we get,
$Z=\sqrt{{{\left( 10-100 \right)}^{2}}+{{120}^{2}}}=150$---(xi)

Substituting the value from equation (xi) to equation (v) we get,
$i=\dfrac{30}{150}=0.2$
So, the peak current is $0.2$ A.

We know for resonant frequency,
$\omega =\dfrac{1}{\sqrt{LC}}$--(xii)

Substituting the values we get,
$\omega =\dfrac{1}{\sqrt{100\times {{10}^{-3}}\times 100\times {{10}^{-6}}}}=100\sqrt{10}$

Now, we know the relation between frequency $f$ and angular frequency $\omega $ as,
$\omega =2\pi f$--(xiii)

Arranging this formula we get,
$f=\dfrac{\omega }{2\pi }=\dfrac{100\sqrt{10}}{2\pi }\approx 50$
So, the resonant frequency is $50$Hz.

Therefore, the correct option is d. $0.2$A and $50$ Hz.

Note: It must be noted that in case of a LCR circuit the total resistance of the circuit comes from the cumulative resistance of the inductor, the capacitor and the resistor linked to the circuit. It is actually known as impedance of the circuit which opposes the flow of current in the LCR circuit.