Derivation and Explanation of Potential Energy of Electric Dipole
Potential energy of electric dipole is a crucial concept in electrostatics, especially for JEE Main Physics. It describes the energy stored due to the orientation of a dipole in an external electric field, and is essential for understanding molecular and atomic behavior under fields.
A classic electric dipole consists of two equal and opposite charges (+q and –q) separated by distance d. The product of charge and separation, p = qd, is called the dipole moment. The dipole's behavior in electric fields reveals deep physical insights relevant to JEE problems.
When an electric dipole is placed in a uniform electric field, it experiences a torque that tries to align it with the field and also possesses potential energy that depends on its orientation with respect to the field direction.
This potential energy has significance in molecular alignment, polar molecule behavior, and forms the basis of many examination questions. Understanding the formula, derivation, and its implications is key for JEE Main aspirants.
Formula for Potential Energy of Electric Dipole
The standard formula for the potential energy of electric dipole in a uniform electric field is:
U = –pE cosθ
where
– U is the potential energy (in joules, J)
– p is dipole moment (C·m)
– E is magnitude of electric field (N/C)
– θ is the angle between dipole moment and field
| Orientation (θ) | U value | Stability |
|---|---|---|
| 0° (along field) | –pE (min) | Stable |
| 90° | 0 | Unstable |
| 180° (opposite field) | +pE (max) | Unstable |
Torque on dipole is mathematically linked to this potential energy since torque tends to lower the energy by aligning the dipole with the field.
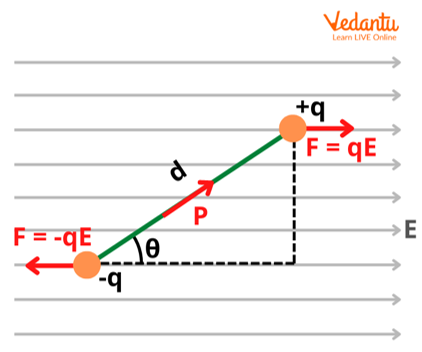
Derivation of Potential Energy of Electric Dipole in Uniform Electric Field
Consider an electric dipole (charges +q, –q separated by d, so moment p = qd) in a uniform field E, inclined at angle θ to the field. The dipole is rotated from θ1 to θ2. The work done against the torque to change orientation is stored as potential energy.
For a small angular displacement dθ, external work done,
ΔW = τ dθ = pE sinθ dθ
Total work from θ1 to θ2:
W = ∫(θ1 to θ2) pE sinθ dθ = –pE [cosθ]θ1θ2
If reference is θ1 = 90°, θ2 = θ, and potential energy is zero at 90°:
U = –pE cosθ
This is the commonly used result for potential energy of electric dipole in uniform electric field.
Physical Interpretation and Graphical View
The sign of U = –pE cosθ determines stability. Minimum potential energy (–pE) occurs when the dipole aligns with the field (θ = 0°), which is stable. Maximum U (+pE) occurs at θ = 180°, making it an unstable equilibrium.
Energy is negative when the dipole aligns with the field, representing a low-energy, stable configuration. Zero energy is when the dipole is perpendicular, and positive when it is opposite the field direction.
A plot of potential energy vs θ shows a cosine curve, minimum at 0° and maximum at 180°.
Typical JEE Numerical Example
Example: A dipole with moment p = 4 × 10–29 C·m is placed in E = 3 × 105 N/C at θ = 60°. Find the potential energy.
U = –pE cosθ
= –(4 × 10–29) × (3 × 105) × 0.5
= –6 × 10–24 J
Final answer: U = –6 × 10–24 J.
Always check angle convention: θ is with respect to E and p, not arbitrary.
- Formula is valid only for uniform electric fields.
- Double-check sign; negative means alignment with field.
- Common errors: missing the negative, angle misinterpretation, or incorrect units.
- Always express answer in SI units (joules).
Applications and Connections to Other JEE Main Topics
Potential energy of electric dipole is vital in molecular physics, dielectric theory, spectroscopy, and capacitor design. It directly links to topics like electric dipole basics, electrostatics, and torque on a dipole in JEE context.
- Electric fields and field lines: Orientation of molecules in fields, influence on sensors.
- Electrostatics mock tests: Practice potential energy numericals.
- Work by torque: Connection between work done and energy.
- Potential and capacitance: How dipole energy affects capacitor behavior.
- Molecular/atomic physics: Real-world relevance.
- Field properties: Understanding dipole alignment and energy changes.
- Contrast with gravitational potential energy: Analogous mathematical structure.
- Experimental skills mock tests: Applying the concept in practical setups.
One pitfall is confusing potential energy of dipole with the energy stored in a capacitor or with gravitational potential energy. Always relate energy changes to dipole orientation in the field for electrostatic case.
A clear grasp of Potential energy of electric dipole enables you to answer direct JEE questions, handle work and torque problems, and build intuition for deeper electrodynamics. For expert-authored stepwise derivations and more solved examples, consult Vedantu’s dedicated JEE Physics learning modules.
FAQs on Potential Energy of Electric Dipole in an Electric Field
2. Why is the potential energy of a dipole negative?
The potential energy is negative when a dipole aligns with the electric field because it is in a stable configuration, having the least energy compared to other orientations.
- Negative energy means work must be done to move the dipole away from equilibrium.
- This stability is essential for understanding dipole behavior in physics and chemistry.
3. When is the potential energy of an electric dipole minimum or maximum?
The potential energy of an electric dipole is minimum when the dipole is parallel to the electric field, and maximum when it is antiparallel.
- Minimum energy at θ = 0°, U = –pE (stable equilibrium).
- Maximum energy at θ = 180°, U = +pE (unstable equilibrium).
4. How does the orientation of the dipole affect its potential energy?
The orientation (angle θ) directly determines the value of potential energy for an electric dipole in an electric field.
- When θ = 0°, dipole is parallel, potential energy is minimum.
- When θ = 180°, dipole is antiparallel, potential energy is maximum.
- At other angles, energy ranges between these two values depending on cos θ.
5. What is the formula for the potential energy of an electric dipole in a uniform electric field?
The standard formula is:
U = –pE cosθ
where:
- U = potential energy
- p = dipole moment (q × 2a)
- E = electric field strength
- θ = angle between dipole moment and field direction
6. What is the significance of potential energy in dipole stability?
Potential energy indicates how stable or unstable a dipole is in an electric field.
- Lower (more negative) potential energy means more stable (aligned parallel to the field).
- Higher (positive) potential energy means unstable (opposite direction).
- This concept helps in predicting molecular orientation and field effects on matter.
7. Can a dipole have positive potential energy in an external field?
Yes, a dipole can have positive potential energy when it is oriented antiparallel (opposite) to the electric field direction.
- This situation occurs when θ = 180°, since cos 180° = -1, and so U = +pE.
- The dipole is in an unstable state and tends to rotate to reduce energy.
8. Is torque needed to calculate potential energy of a dipole?
No, the potential energy can be calculated directly from the formula without finding torque, but torque and potential energy are related.
- Torque (τ) = pE sinθ acts to rotate the dipole towards minimum energy position.
- Knowing one can help understand the behavior and equilibrium of the dipole.
9. How does potential energy relate to the work done in rotating a dipole?
The work done in rotating a dipole in an electric field equals the change in its potential energy.
- Work done = Final potential energy – Initial potential energy
- This principle helps solve many JEE/NEET numerical problems.
10. Does the potential energy of a dipole change if the magnitude of the dipole moment changes?
Yes, the potential energy is directly proportional to the dipole moment.
- If the dipole moment (p) increases, the magnitude of potential energy (U = –pE cosθ) increases.
- This is relevant when considering molecules or atoms with variable dipole moments in fields.
11. Why is potential energy not always zero when the field is present?
The potential energy of a dipole depends on its angle with the electric field, not just the field's presence.
- Only at θ = 90° (perpendicular), U = 0.
- At other angles, the value depends on cosθ, so U is usually nonzero.
