




How Does a Movable Pulley Make Work Easier?
A movable pulley is a simple machine where the pulley wheel is attached to the load and moves with it, reducing the effort required to lift heavy objects. This concept is significant in understanding force multiplication in mechanical systems and is essential for competitive exams like JEE Main.
Movable Pulley Definition and Principle
A movable pulley consists of a wheel fixed to a block that is not stationary. Instead, the pulley block moves with the load as it is lifted. The main function is to provide mechanical advantage, making it easier to raise objects using a lesser force compared to lifting them directly.
Unlike a fixed pulley, which is anchored and only changes the direction of the applied force, a movable pulley reduces the effort required but does not alter the force direction. The pulley and load are both displaced when the rope is pulled.
Movable Pulley vs Fixed Pulley
The distinction between movable and fixed pulleys is fundamental in mechanics. Comparison based on key features aids in conceptual clarity, particularly in solving pulley-based problems in physics examinations.
| Aspect | Movable Pulley |
|---|---|
| Wheel Position | Moves with the load |
| Mechanical Advantage (Ideal) | 2 |
| Force Direction Change | No |
| Effort Reduction | Yes |
| Use Case | Cargo lifts, cranes |
Movable Pulley Diagram and Force Distribution
In the standard setup, a single movable pulley is attached to the load. The rope runs over a fixed support, while both ends of the rope may be fixed or one end may be pulled by the applied effort. Force distribution is such that the load is supported equally by the rope segments passing through the pulley.
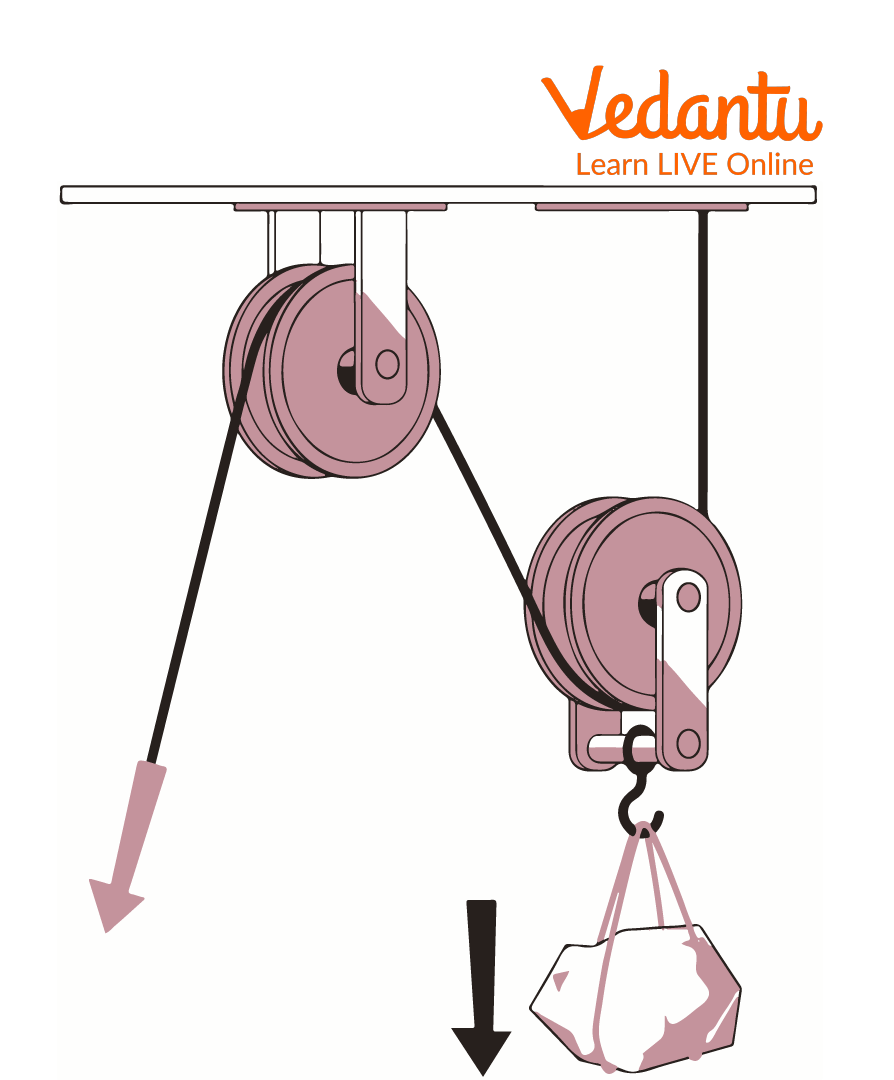
If the mass of the pulley and rope is neglected, and friction is absent, the tension is the same in all segments of the rope. This results in equal sharing of the load between the rope segments supporting the movable pulley. Further understanding of such arrangements is crucial for solving pulley-related problems in the context of the Pulley System .
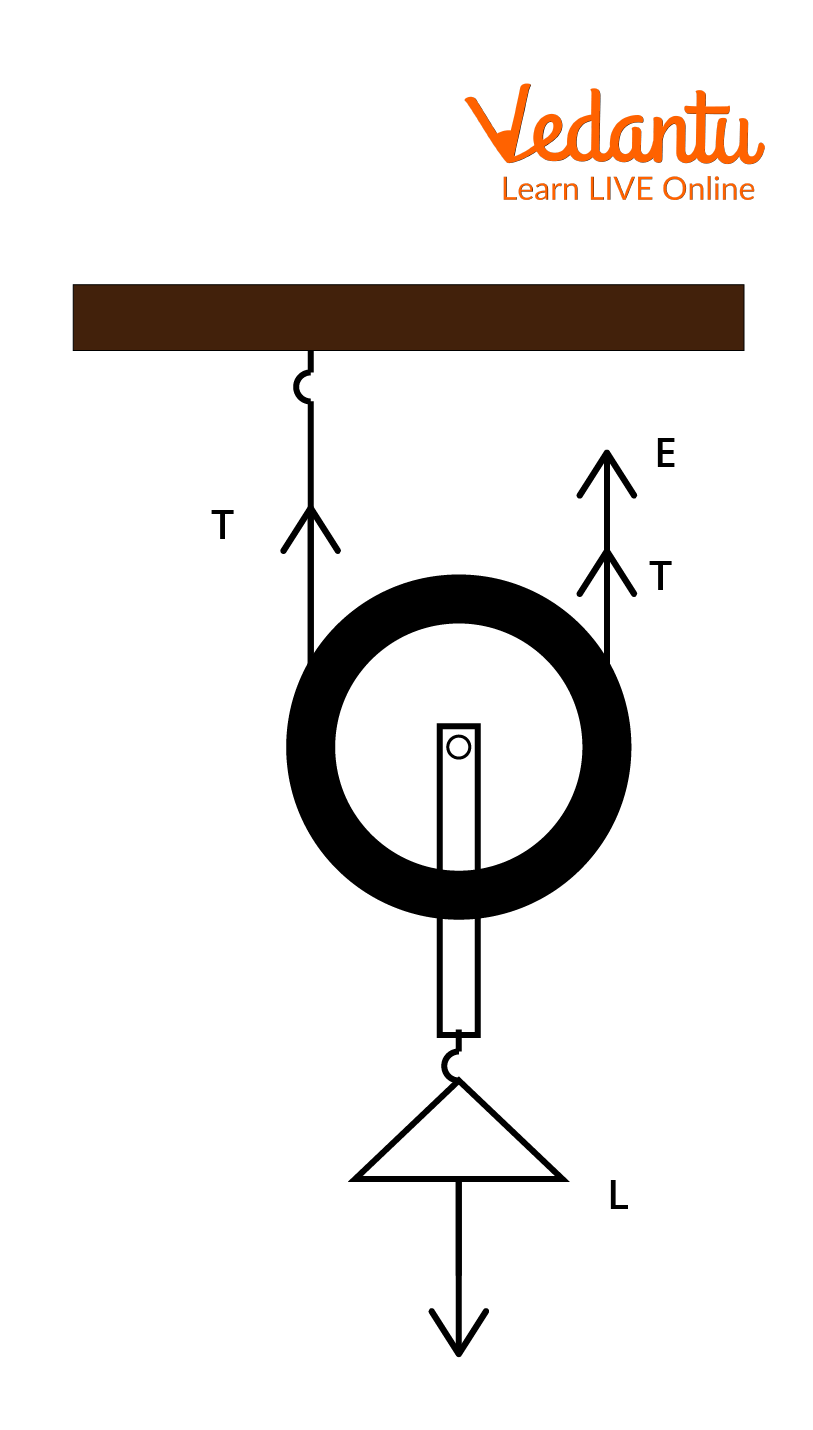
Mechanical Advantage of Movable Pulley
Mechanical advantage (MA) is defined as the ratio of load lifted ($W$) to the effort applied ($P$). For a single ideal movable pulley, both rope segments directly support the load, hence:
$MA = \dfrac{W}{P}$
In the ideal case (frictionless and massless rope/pulley), $MA = 2$. This means the effort required is half of the load. For example, for $W = 200\,N$, the effort $P = W/2 = 100\,N$.
Block and Tackle: Compound Movable Pulley Systems
A block and tackle system consists of multiple movable and fixed pulleys assembled together. This system allows further increase in mechanical advantage, reducing the force to lift loads well beyond those manageable by a single movable pulley.
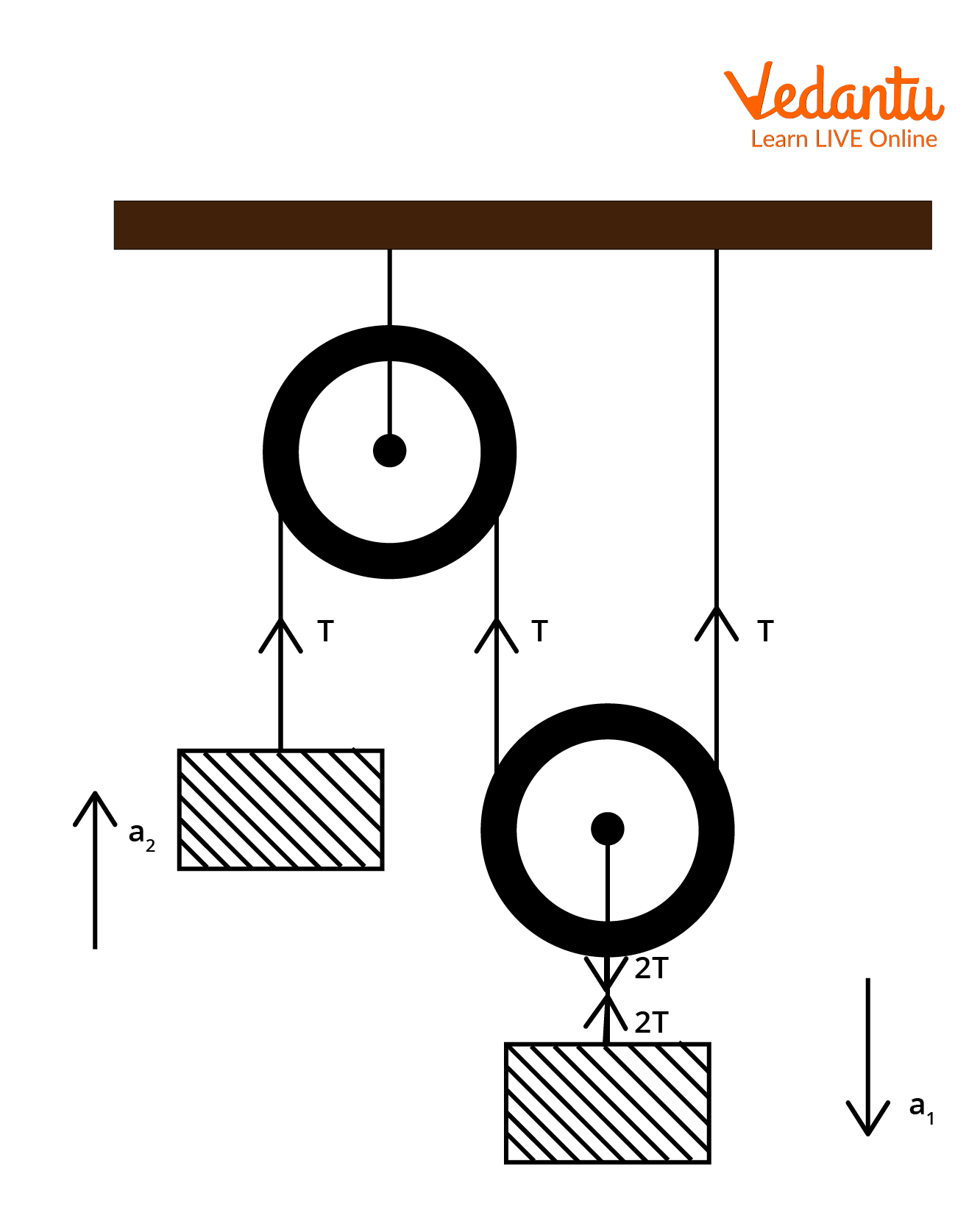
The total mechanical advantage in a block and tackle arrangement is equal to the number of rope segments directly supporting the load. Such systems are commonly used in construction cranes and heavy lifting devices. Related details can be explored in the Block And Tackle System.
Applications and Examples of Movable Pulleys
Movable pulleys are applied in various mechanical and daily life contexts. They are used in construction sites for lifting materials, in elevators, gym equipment, and certain hoisting devices. In the human body, the patella acts as a movable pulley, enhancing the efficiency of leg movement.
Examples of movable pulley systems include cargo elevators, window blind systems, sailing rigs, and compound hoists. The patella (kneecap) modifies the direction and magnitude of force transmitted by muscles, serving as a biological movable pulley.
For deeper understanding of work done against gravity and force transfer in such machines, refer to Work, Energy And Power.
Advantages and Disadvantages of Movable Pulley Systems
The use of a movable pulley offers key mechanical benefits but also presents real-world limitations. These must be considered in both theoretical analysis and practical applications encountered in physics problems.
| Advantages | Disadvantages |
|---|---|
| Effort needed is greatly reduced | Pulley moves with load, less stable setup |
| Mechanical advantage is 2 (ideal) | Does not change effort force direction |
| Easily combined with other pulleys | Friction reduces practical efficiency |
Key Concepts for Solving Movable Pulley Questions
Accurate problem solving in exam scenarios requires identification of all rope segments supporting the load and correct application of the mechanical advantage formula. If friction or pulley/rope masses are non-negligible, mechanical advantage reduces below the ideal value.
Careful labeling of diagrams, assignment of force directions, and clear calculation steps enhance accuracy and scoring in both numerical and theoretical problems. Practice with different configurations is recommended for mastery in competitive exams. Related differences can be studied in Motor And Generator.
Summary: Core Properties of Movable Pulleys
- Pulley moves with the load being lifted
- Reduces effort without changing force direction
- Mechanical advantage is ideally 2
- Actual efficiency affected by friction and rope/pulley mass
- Used in cranes, elevators, and gym machines
Understanding movable pulley systems is essential for analysing simple machines, force transfer, and work efficiency at JEE and board exam levels. Related force concepts are explored further under Centrifugal Force and for gravitational effects at Acceleration Due To Gravity.
FAQs on What Is a Movable Pulley?
1. What is a movable pulley?
A movable pulley is a simple machine that can move along the rope or cable attached to a fixed point, which is used to change the direction and magnitude of the force applied.
Main features:
- Attached to the load, not to a fixed position
- Reduces the amount of input force needed
- Often used to lift heavy objects with less effort
2. What are the uses of movable pulley?
Movable pulleys are widely used in systems that require lifting or moving heavy loads while reducing the effort needed.
Common uses include:
- Lifting buckets from wells
- Construction cranes and hoists
- Elevators and lifts
- Gym weight machines
- Mechanical rescue operations
3. How does a movable pulley make work easier?
A movable pulley makes work easier by reducing the input force needed to lift a load.
This is achieved by:
- Sharing the weight of the load between two sections of the rope
- Providing a mechanical advantage (usually 2 for a single movable pulley)
- Allowing a smaller force to lift a heavier object
4. What is the mechanical advantage of a movable pulley?
The mechanical advantage (MA) of a single movable pulley is usually 2.
This means:
- The effort required is half the load weight
- The input force is distributed via the pulley system
5. What is the difference between a fixed pulley and a movable pulley?
A fixed pulley only changes the direction of force, while a movable pulley reduces the amount of force needed.
Key differences:
- Fixed pulley is attached to a fixed support; movable pulley moves with the load
- Movable pulley provides mechanical advantage; fixed pulley doesn't
- Movable pulleys are used for lifting heavier objects with less effort
6. Can you give an example of a movable pulley system found in daily life?
A commonly seen movable pulley system is a construction crane.
Other daily life examples include:
- Elevator mechanisms
- Wells for drawing water
- Gym machines for weight lifting
- Rescue equipment like pulleys in fire brigade for lifting stretchers
7. What is the formula for mechanical advantage in a movable pulley?
The mechanical advantage (MA) of a movable pulley is calculated by dividing the load by the effort:
MA = Load / Effort
- For a single movable pulley, MA is typically 2.
- This means the force needed to lift the load is halved.
8. Why does a movable pulley provide more mechanical advantage than a fixed pulley?
A movable pulley provides more mechanical advantage because it reduces the force required to lift an object.
Reasons include:
- The rope supports the load at two points
- The effort is distributed, effectively halving the required force
- It combines with fixed pulleys in block and tackle systems for even greater advantage
9. What are the limitations of a movable pulley?
Movable pulleys have some limitations despite their advantages.
Limitations:
- Increased rope length and movement needed
- Requires stable support for the rope
- More complex setup compared to fixed pulleys
- Pulley weight adds to load being lifted
10. How does combining a fixed pulley and a movable pulley help?
Combining fixed and movable pulleys creates a block and tackle system, which provides a higher mechanical advantage for lifting heavy loads.
Benefits:
- Reduces the effort needed further
- Makes direction and magnitude of force manageable
- Used in cranes, ships, and construction sites
- Enables lifting of very heavy objects with much less force
























