




Gauss Law Formula and How to Use It with Examples
Gauss Law is a fundamental principle in electrostatics that relates the total electric flux passing through a closed surface to the net charge enclosed by that surface. This law simplifies the calculation of electric fields for systems with a high degree of symmetry and is essential for advanced problem-solving in physics, especially for JEE aspirants.
Statement of Gauss Law
Gauss Law states that the total electric flux passing through any closed surface is equal to the net electric charge enclosed by the surface divided by the permittivity of free space. Mathematically, it is expressed as:
$\phi_E = \dfrac{Q_{\text{enclosed}}}{\varepsilon_0}$
Here, $\phi_E$ is the total electric flux through the surface, $Q_{\text{enclosed}}$ is the net charge enclosed, and $\varepsilon_0$ is the permittivity of free space. Detailed understanding of electric flux is important for applying Gauss Law accurately. For more foundational understanding, refer to Understanding Electric Field Lines.
Important Terms in Gauss Law
Electric flux represents the number of electric field lines passing through a given surface. It is a measure of the 'flow' of the electric field through a surface and is given by:
$\phi_E = \int \vec{E} \cdot d\vec{A}$
Here, $\vec{E}$ is the electric field vector, $d\vec{A}$ is the vector area element, and the dot product denotes that only the component of $\vec{E}$ normal to the surface contributes to the flux.
Mathematical Form of Gauss Law
The integral form of Gauss Law for the electric field is:
$\oint_{S} \vec{E} \cdot d\vec{A} = \dfrac{Q_{\text{enclosed}}}{\varepsilon_0}$
This equation states that the closed surface integral of the electric field, i.e., the total electric flux through the surface, equals the net charge inside the surface divided by the permittivity of free space. The closed surface is often referred to as a Gaussian surface. Understanding the choice of Gaussian surfaces is crucial when calculating electric fields for various charge configurations. For a deeper conceptual overview, see Introduction To Electrostatics.
Choosing a Gaussian Surface
A Gaussian surface is an imaginary closed surface over which Gauss Law is applied. The selection of this surface depends on the symmetry of the charge distribution. The correct choice greatly simplifies the calculation of the electric field.
- The surface must be closed and continuous
- The symmetry of the surface should match the symmetry of the charge distribution
- The electric field should have a constant magnitude over the surface, or be zero where not needed
Derivation of Gauss Law for a Point Charge
Consider a point charge $+q$ placed at the centre of a sphere of radius $r$. The electric field at any point on the sphere is given by:
$E = \dfrac{q}{4\pi \varepsilon_0 r^2}$
The total electric flux through the spherical surface is:
$\phi_E = E \cdot 4\pi r^2 = \dfrac{q}{\varepsilon_0}$
This result shows that the total electric flux depends only on the charge enclosed and not on the radius of the sphere. The derivation confirms that Gauss Law holds for any closed surface enclosing the charge.
Applications of Gauss Law
Gauss Law is especially useful for finding electric fields created by symmetrical charge distributions. Typical applications include infinite lines of charge, infinite plane sheets, and spherical shells. A correct application of Gauss Law involves careful selection of the Gaussian surface. For systematic revision, refer to Electrostatics Revision Notes.
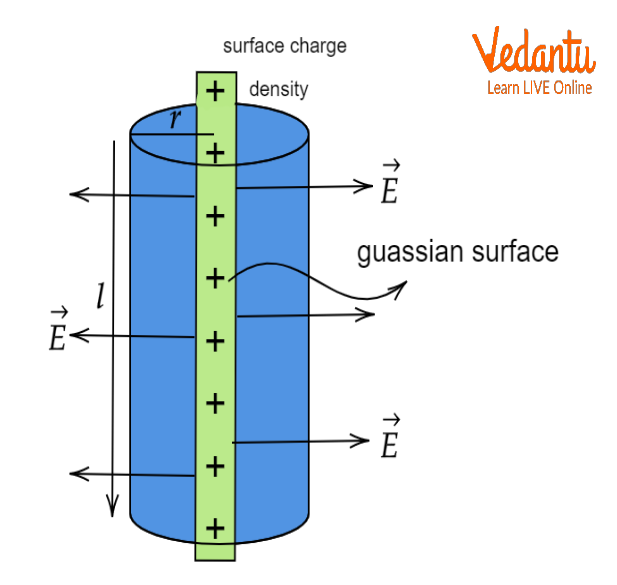
Electric Field Due to an Infinitely Long Charged Wire
For an infinitely long straight wire carrying linear charge density $\lambda$, the electric field at distance $r$ from the wire is given by:
$E = \dfrac{\lambda}{2\pi \varepsilon_0 r}$
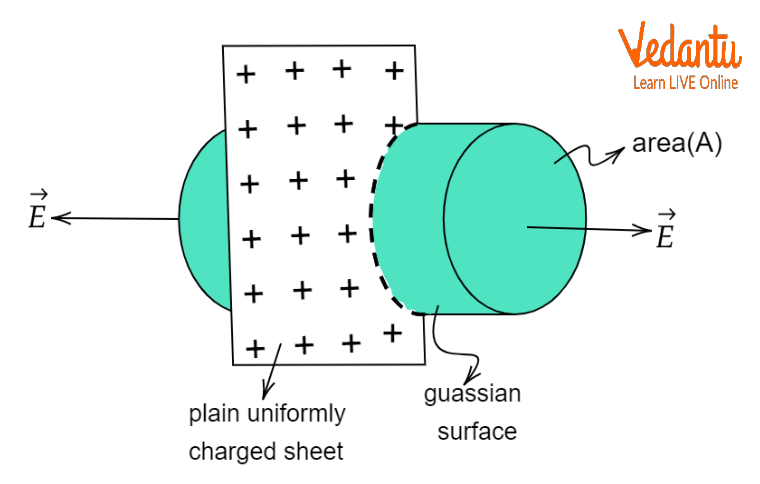
Electric Field Due to a Uniformly Charged Infinite Plane Sheet
For an infinite plane sheet with surface charge density $\sigma$, the electric field at any point near the sheet is:
$E = \dfrac{\sigma}{2\varepsilon_0}$
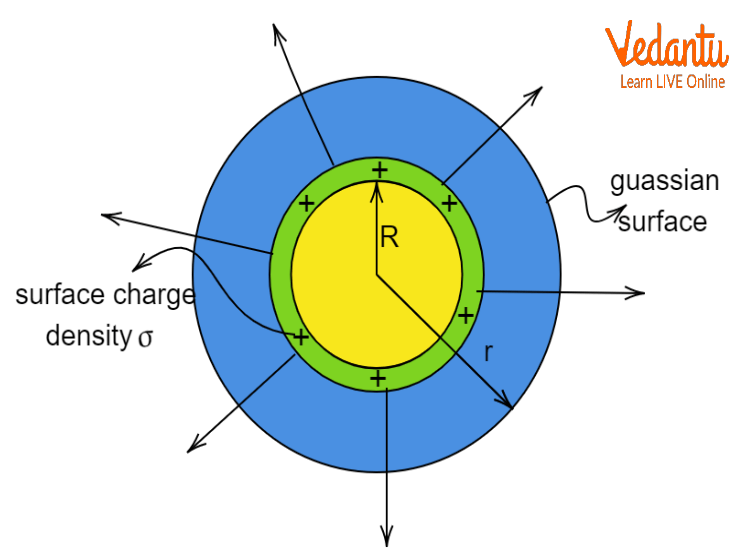
Electric Field Due to a Uniformly Charged Thin Spherical Shell
For a spherical shell of total charge $q$ and radius $R$:
- At a point outside ($r \geq R$): $E = \dfrac{q}{4\pi\varepsilon_0 r^2}$
- At a point inside ($r < R$): $E = 0$
Gauss Law: Differential Form
The differential form of Gauss Law establishes the local relationship between electric field and charge density. It is written as:
$\vec{\nabla} \cdot \vec{E} = \dfrac{\rho}{\varepsilon_0}$
Here, $\vec{\nabla} \cdot \vec{E}$ denotes the divergence of electric field, and $\rho$ is the volume charge density at a given point.
Summary Table: Gauss Law for Different Geometries
| Geometry | Electric Field |
|---|---|
| Infinite Line of Charge | $E = \dfrac{\lambda}{2\pi\varepsilon_0 r}$ |
| Infinite Plane Sheet | $E = \dfrac{\sigma}{2\varepsilon_0}$ |
| Outside Spherical Shell | $E = \dfrac{q}{4\pi\varepsilon_0 r^2}$ |
| Inside Spherical Shell | $E = 0$ |
Key Properties and Limitations of Gauss Law
Gauss Law is valid for all electric fields and charge distributions, but it is most useful for cases with sufficient symmetry. For non-symmetric cases, application of Gauss Law may not simplify calculations significantly. To understand the properties of electric field lines and their implications, see Electric Field Lines and Their Properties.
Other Related Gauss Laws in Physics
In addition to Gauss Law for the electric field, similar laws exist in other domains, such as Gauss Law for magnetism and Gauss Law for gravity. Gauss Law for magnetism states that the net magnetic flux through any closed surface is always zero, implying the absence of magnetic monopoles.
- Gauss Law for gravity involves the gravitational field and mass enclosed
- All Gauss Laws use the concept of flux through closed surfaces
Conclusion on Gauss Law
Gauss Law establishes a direct relationship between the total electric flux and the net enclosed charge. It is fundamental for understanding charge distributions and electric field patterns in electrostatics. For concepts related to potential difference and capacitance, explore Understanding Potential Difference and Concepts of Capacitance.
FAQs on Understanding Gauss Law in Physics
1. What is Gauss's Law?
Gauss's Law states that the total electric flux through a closed surface is equal to 1/ε₀ times the net electric charge enclosed within the surface.
Key points:
- Expressed mathematically as ∮E·dA = Qencl/ε₀
- It is a fundamental law of electrostatics
- Applies to all closed surfaces (Gaussian surfaces)
2. State Gauss's Law with formula.
Gauss's Law states that the electric flux through any closed surface is equal to the enclosed charge divided by permittivity of free space (ε₀).
Formula:
- ∮E·dA = Qencl / ε₀
- Where E is the electric field, dA is the infinitesimal area element, and Qencl is the enclosed charge.
3. What is the significance of Gauss's Law?
Gauss's Law is significant because it simplifies calculations of electric fields for symmetric charge distributions.
Key implications:
- Makes solving electric fields easier for spherical, cylindrical, and planar symmetries
- Relates electric flux to enclosed charge
- Foundational to Maxwell's equations in electromagnetism
4. What is a Gaussian surface?
A Gaussian surface is an imaginary closed surface used in applying Gauss's Law to calculate electric fields.
Properties:
- Chosen to match the symmetry of the charge distribution
- Can be spherical, cylindrical, or planar, depending on the problem
- Helps make calculations simpler and more direct
5. How do you use Gauss's Law to find the electric field due to a point charge?
To find the electric field of a point charge using Gauss’s Law, select a spherical Gaussian surface centered on the charge.
Steps:
- The surface is a sphere of radius r around the charge Q
- By symmetry, electric field E is constant at every point on the sphere and points radially outward
- Electric flux = E × 4πr²
- Gauss’s Law: E × 4πr² = Q/ε₀ ⇒ E = Q/(4πε₀r²)
6. List applications of Gauss’s Law in daily life or technology.
Gauss's Law is used in both theoretical and practical situations.
Examples:
- Calculating electric field in conductors and capacitors
- Explaining phenomena like shielding inside hollow conductors (Faraday cages)
- Designing devices like coaxial cables and sensors
- Understanding charge distribution in static electricity problems
7. Why is Gauss's Law not always suitable for every charge configuration?
Gauss's Law is not always convenient if the charge distribution lacks symmetry, making it difficult to select a suitable Gaussian surface.
Key challenges:
- Asymmetric charge distributions
- Difficulty in calculating total electric flux
- Preferable for problems with spherical, cylindrical, or planar symmetry
8. What is meant by electric flux?
Electric flux is the measure of the number of electric field lines passing through a given surface.
Important facts:
- Represented by the symbol ΦE
- Formula: ΦE = E·A·cosθ, where θ is the angle between E and area vector
- Measured in Newton-meter²/Coulomb (N·m²/C)
9. How does Gauss’s Law relate to Coulomb’s Law?
Gauss's Law can be used to derive Coulomb’s Law for point charges.
Relationship:
- By applying Gauss’s Law to a point charge, you obtain the same expression as Coulomb’s Law
- Shows consistency between both laws for electrostatics
- Highlights that field calculation via symmetry leads to Coulomb’s result
10. Can Gauss's Law be used for gravitational fields?
Yes, a similar form of Gauss's Law applies to gravitational fields.
Analogies:
- Flux of the gravitational field through a closed surface is proportional to the enclosed mass
- Shows that field lines behave similarly in both gravitational and electric fields
- Helpful for deriving field expressions in gravitation
























