Understanding Union, Intersection, and Difference of Sets

The topic "Union Intersection And Difference Of Sets" falls under TYPE A — Core Concept Pages, as it is a foundational part of the syllabus in JEE Mathematics. It covers essential operations on sets, crucial for understanding more advanced topics in mathematics and for problem-solving in competitive exams.

Purpose and Scope of Set Operations: Union, Intersection, and Difference

Set operations are foundational in mathematics. They enable the combination, comparison, and separation of sets based on membership. Analyzing these operations assists in describing relations, functions, and solving problems involving sets in advanced mathematics and competitive exams.

Core Idea Before Formalism: Intuitive Understanding

The union of sets combines all elements from the involved sets, ensuring duplication is avoided. The intersection identifies common elements shared by the sets. The difference extracts elements present in one set but not in another, clarifying exclusive membership.

Definitions and Standard Notation

Let $A$ and $B$ denote non-empty sets under a universal set $U$. The key set operations are:

• Union of sets
• Intersection of sets
• Difference of sets
• Complement of a set

The union of $A$ and $B$ is denoted as $A \cup B$. The intersection is $A \cap B$. The difference is $A - B$ or $A \setminus B$. The complement is $A^{c}$ or $\overline{A}$, relative to $U$.

Formal Properties and Results

The following properties hold for all subsets $A,B,C \subseteq U$.

• Commutative laws for union and intersection
• Associative laws for union and intersection
• Distributive laws
• De Morgan’s laws
• Identity elements
• Difference is not commutative

For every $A$ and $B$, $A \cup B = B \cup A$, and $A \cap B = B \cap A$ hold.

Associativity ensures $(A \cup B) \cup C = A \cup (B \cup C)$. Similarly, $(A \cap B) \cap C = A \cap (B \cap C)$.

Distributive property: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, and $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$.

De Morgan’s laws state $(A \cup B)^{c} = A^{c} \cap B^{c}$ and $(A \cap B)^{c} = A^{c} \cup B^{c}$.

For all $A$, $A \cup \varnothing = A$ and $A \cap \varnothing = \varnothing$. $\varnothing$ denotes the empty set.

$A - B$ is not generally equal to $B - A$.

Key Formulas for Union, Intersection, and Difference

For finite sets $A$ and $B$:

The number of elements in $A \cup B$ is $n(A \cup B) = n(A) + n(B) - n(A \cap B)$.

For the difference, $n(A - B) = n(A) - n(A \cap B)$.

For three sets, $n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C)$.

Worked Example 1: Direct Union Evaluation

Given $A = \{1, 2, 3, 4\}$ and $B = \{2, 4, 5, 6\}$. Find $A \cup B$.

First, combine all elements from both sets:

$A \cup B = \{1, 2, 3, 4, 2, 4, 5, 6\}$

Remove duplicates:

$A \cup B = \{1, 2, 3, 4, 5, 6\}$

Worked Example 2: Intersection of Sets

Given $A = \{3, 5, 7, 9\}$ and $B = \{5, 7, 11\}$, determine $A \cap B$.

Identify common elements:

$A \cap B = \{5, 7\}$

Worked Example 3: Difference and Complement

Let $U = \{a, b, c, d, e\}$, $A = \{b, c, d\}$, and $B = \{c, e\}$. Find $A - B$ and $A^{c}$.

First, determine $A - B$:

$A - B = \{b, d\}$

Next, $A^{c} = U - A$:

$A^{c} = \{a, e\}$

Worked Example 4: Using Set Identities

Let $A = \{1, 2, 3, 4\}$ and $B = \{3, 4, 5, 6\}$, $C = \{2, 3, 5\}$. Compute $(A \cap B) \cup (B \cap C)$.

First, find $A \cap B$:

$A \cap B = \{3, 4\}$

Next, $B \cap C = \{3, 5\}$

Now, calculate the union:

$(A \cap B) \cup (B \cap C) = \{3, 4, 5\}$

Common Student Misconceptions in Set Operations

• Confusing union with intersection
• Repeating elements in unions
• Assuming difference is commutative
• Ignoring universal set in complements
• Incorrect De Morgan application

Typical JEE Pattern for Questions on Set Operations

• Direct computation from given sets
• Application of union-intersection identities
• Problems using Venn diagrams
• Cardinality formula application
• Proof-based assertions on sets

Cartesian Product and Advanced Set Structures

The Cartesian product $A \times B = \{(a, b) \mid a \in A,\, b \in B\}$ forms ordered pairs. For example, $\mathbb{R}^2 = \mathbb{R} \times \mathbb{R}$ denotes the plane consisting of all ordered pairs of real numbers.

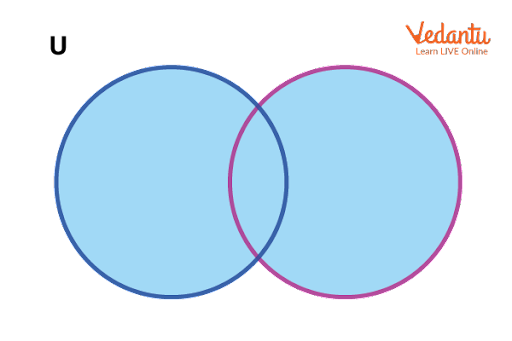
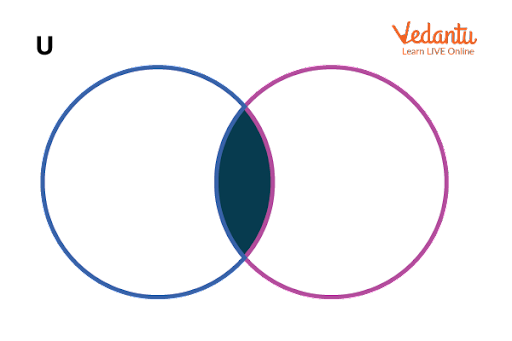
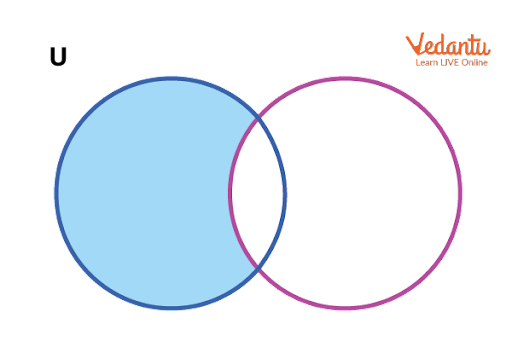
Representation of Set Operations Using Venn Diagrams

Venn diagrams visually illustrate the outcomes of union, intersection, and difference. Shaded regions indicate the resultant sets for each operation, aiding comprehension.

For extended study of sets, refer to Sets, Relations, And Functions, which provides foundational set theory required for JEE-level mathematics.