How to Calculate the Sum of an Infinite Geometric Progression

The sum of an infinite geometric progression (GP) is defined for common ratios whose absolute value is less than one, resulting in a finite sum for the series. The formal structure, derivation, and evaluation techniques are fundamental in advanced mathematics and competitive exam contexts such as JEE.

General Form and Notation of the Infinite Geometric Progression

Definition: A geometric progression is an ordered set $\{a, ar, ar^2, ar^3, \ldots\}$ where $a \neq 0$ is the first term and $r$ $(r \neq 0)$ is the common ratio, constant for all terms. The infinite GP sum refers to summing all terms as $n \to \infty$.

The sum of the first $n$ terms of a GP is denoted by $S_n = a + ar + ar^2 + \ldots + ar^{n-1}$, with the formula $S_n = a \frac{1 - r^n}{1 - r}$, $r \neq 1$. In the infinite case, $S_\infty = \lim_{n \to \infty} S_n$.

Derivation of the Infinite Geometric Progression Sum ($|r| < 1$)

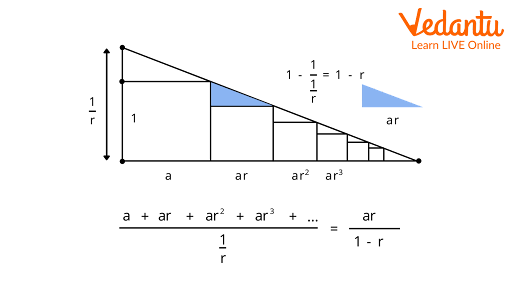
To derive the sum, consider $S = a + ar + ar^2 + ar^3 + \cdots$ with $|r| < 1$. Multiply both sides by $r$ to get $rS = ar + ar^2 + ar^3 + \cdots$. Subtracting, $S - rS = a$.

This gives $S(1 - r) = a$. Upon division, $S = \frac{a}{1 - r}$. Thus, the infinite GP sum converges only when $|r| < 1$.

Convergence Criteria for the Sum of an Infinite Geometric Series

The convergence of $S_\infty$ depends entirely on the common ratio. If $|r| \geq 1$, the terms do not approach zero, so the sum diverges. If $|r| < 1$, $r^n \to 0$ as $n \to \infty$, allowing the finite sum formula to simplify.

For $|r| < 1,$ $\lim_{n \to \infty} a r^n = 0,$ so $S_\infty = a/(1 - r)$ is strictly defined. For $|r| \geq 1$, the sum does not exist in the finite sense.

Formula Specification and Variable Roles in Infinite GP Sum

For $\{a, ar, ar^2, \ldots\}$, the result is $S_\infty = a/(1 - r)$, valid only if $|r| < 1$. Here, $a$ is the initial term, and $r$ is the constant ratio. If $|r| \geq 1$, the sum diverges to infinity or minus infinity, depending on the sign of $a$ and $r$.

Evaluation of Sums for Specific Infinite GP Series

For direct calculation, ensure to verify $|r| < 1$ before applying the sum formula. Cases with $|r| = 1$ (e.g., $r = 1$ or $r = -1$) are undefined in the context of convergence.

Illustrative Examples for Infinite GP Summation

Example: $S = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots$
Here, $a = 1$, $r = \frac{1}{2}$, so $|r| = \frac{1}{2} < 1$.
Substitute: $S = \frac{1}{1 - \frac{1}{2}} = 2$

Example: $S = 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \cdots$
Given $a = 1$, $r = -\frac{1}{2}$, so $|r| = \frac{1}{2} < 1$.
Compute: $S = \frac{1}{1-(-\frac{1}{2})} = \frac{1}{1.5} = \frac{2}{3}$

Example: $S = \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \cdots$
Here, $a = \frac{1}{3}$, $r = \frac{1}{3}$.
Calculate: $S = \frac{\frac{1}{3}}{1 - \frac{1}{3}} = \frac{\frac{1}{3}}{\frac{2}{3}} = \frac{1}{2}$

Example: $S = 3 - 6 + 12 - 24 + \cdots$
Here, $a = 3$, $r = -2$.
Since $|r| = 2 \geq 1$, the series diverges and the sum is not defined.

Example: $S = \frac{1}{3} + \frac{1}{25} + \frac{1}{27} + \frac{1}{625} + \cdots$
Group as two interleaved series.
First: $a_1 = \frac{1}{3}$, $r_1 = \frac{1}{9}$, yields $S_1 = \frac{\frac{1}{3}}{1 - \frac{1}{9}} = \frac{3}{8}$.
Second: $a_2 = \frac{1}{25}$, $r_2 = \frac{1}{25}$, gives $S_2 = \frac{\frac{1}{25}}{1 - \frac{1}{25}} = \frac{1}{24}$.
Final result: $S = \frac{3}{8} + \frac{1}{24} = \frac{10}{24} = \frac{5}{12}$.

Characteristic Misconceptions and Divergent Cases in Infinite GP

A common error is to apply the sum formula without checking if $|r| < 1$. For $|r| \geq 1$, terms remain large or oscillatory, and the sum formula is invalid. When $r=1$, consecutively added terms cannot form a finite sum.

For advanced practice on related topics, refer to Sum To Product Formulae and explore additional links to strengthen foundational skills.

• Standard form of infinite GP
• Convergence criterion for $|r|$
• Finite sum when $|r| < 1$
• Divergence when $|r| \geq 1$
• Stepwise sum derivation
• Representative worked examples
• Interleaved series evaluation