The Fundamental Counting Principle of Multiplication is a foundational result in combinatorics used to count the total number of ways to perform a sequence of operations, where each operation is independent of the previous ones. This principle forms the basis for advanced topics such as permutations, combinations, and probability calculations in JEE Main and related examinations.

Mathematical Statement and Structure of the Fundamental Counting Principle of Multiplication

The Fundamental Counting Principle of Multiplication (also known as the multiplication rule for counting) states that: If a process consists of $k$ independent steps, and if the first step can be performed in $n_1$ ways, the second step in $n_2$ ways, ..., and the $k$th step in $n_k$ ways, then the total number of possible outcomes for the entire process is given by the product $n_1 \times n_2 \times \cdots \times n_k$.

Formally, for $k \in \mathbb{N}$ and positive integers $n_1, n_2, \ldots, n_k$, the total number of ordered tuples $(a_1, a_2, \ldots, a_k)$ such that $a_1$ can be chosen in $n_1$ ways, $a_2$ can be chosen in $n_2$ ways independently of $a_1$, and so on, is:

$\boxed{n_1 \times n_2 \times \cdots \times n_k}$

This result is foundational for topics such as Permutations And Combinations.

Explanation of Independent and Sequential Choices in the Multiplication Rule

In the context of the multiplication principle, the choices or steps must be independent. This means that the number of options available at each step does not depend on the choices made in previous steps, unless explicitly restricted. Each operation or selection is performed consecutively, and each is counted across all possibilities of the previous steps.

If, for instance, a process consists of two consecutive choices: the first choice can be performed in $m$ ways and for every fixed outcome of the first, the second can be performed in $n$ ways, then the total number of ordered pairs is $m \times n$.

Distinction Between Multiplication Principle and Addition Principle in Counting

The multiplication principle applies strictly to situations modeled by "AND" statements—where two or more independent tasks are performed in sequence and the total requires combining all possibilities. In contrast, the addition principle counts disjoint outcomes described by "OR" statements, where tasks are mutually exclusive, and the total number of ways is the sum of the separate counts.

For process with mutually exclusive actions $A$ (possible in $n_1$ ways) or $B$ (possible in $n_2$ ways), total possibilities are $n_1 + n_2$. For process involving actions $A$ (possible in $n_1$ ways) and $B$ (possible in $n_2$ ways, after $A$), total possibilities are $n_1 \times n_2$.

Further details on the distinction and joint use of these principles can be found at Fundamental Principle Of Counting.

Stepwise Derivation of the Fundamental Counting Principle of Multiplication

Consider a process involving $k$ sequential steps, labelled $S_1, S_2, \ldots, S_k$.

Step 1: The first step, $S_1$, can be performed in $n_1$ ways.

Step 2: For each way of performing $S_1$, the second step, $S_2$, can be performed in $n_2$ ways independently. Thus, after two steps, the total number of ways = $n_1 \times n_2$.

Step 3: For each way of performing the first two steps, the third step, $S_3$, can be performed in $n_3$ ways independently. Thus, after three steps, the total number of ways = $n_1 \times n_2 \times n_3$.

Step 4: Proceeding in this fashion, after $k$ such independent steps, the number of ways is given recursively as:

Let $W_1 = n_1$.

After step 2: $W_2 = W_1 \times n_2 = n_1 n_2$.

After step 3: $W_3 = W_2 \times n_3 = n_1 n_2 n_3$.

...

After step $k$: $W_k = W_{k-1} \times n_k = n_1 n_2 \cdots n_k$.

Therefore, the total number of possible ordered outcomes is the product $n_1 n_2 \cdots n_k$.

Worked Example 1: Counting Digit Codes with Repetition Allowed

Given: Construct a 4-digit code where each digit can be any numeral from 0 to 9, and the same digit may be used more than once.

Step 1 (First digit): 10 choices (0 through 9)

Step 2 (Second digit): 10 choices (independent of the first)

Step 3 (Third digit): 10 choices (independent of the previous)

Step 4 (Fourth digit): 10 choices (independent)

Calculation: Total codes = $10 \times 10 \times 10 \times 10 = 10^4 = 10000$.

Final result: The number of possible 4-digit codes is $10000$.

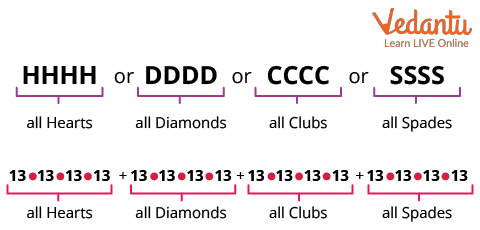
Worked Example 2: Selecting Cards from the Same Suit with Repetitions

Given: Four cards are chosen from a standard 52-card deck, with replacement, all from the same suit.

Step 1: There are 4 possible suits (hearts, clubs, spades, diamonds).

Step 2: For a fixed suit, each card can be any of the 13 values, and replacement allows repetition.

Step 3: For each card selection within the fixed suit: 13 choices for the first card, 13 for the second, 13 for the third, 13 for the fourth.

Step 4: Total for one suit: $13 \times 13 \times 13 \times 13 = 28561$.

Step 5: Across all suits, multiply by 4: $28561 \times 4 = 114244$.

Final result: The required number of sequences is $114244$.

Worked Example 3: Arranging Books on a Shelf of Different Subjects

Given: Place one Physics, one Chemistry, and one Mathematics book (all distinct) on a shelf; the order matters.

Step 1 (Physics): 1 way (only one Physics book)

Step 2 (Chemistry): 1 way (only one Chemistry book)

Step 3 (Mathematics): 1 way (only one Mathematics book)

Step 4: The possible arrangements are permutations of three distinct books: $3! = 6$ ways.

Final result: There are $6$ ways to arrange these books.

For more examples involving arrangement and selection, refer to Probability Fundamentals.

Special Cases and Cautions in the Application of the Multiplication Principle

If certain selections are not independent (for instance, without replacement, or if extra constraints are imposed such as “no digit repeats”), the multiplication principle must be carefully modified. When restrictions reduce the number of options as steps progress, at each step the correct count must be specified to ensure correctness.

In the case of repeated items or when arrangement requires all items to be distinct, the total number of ways is not simply the product, but must be adjusted to account for reductions at each step.

Frequently Asked Questions on the Fundamental Counting Principle of Multiplication

Does the Fundamental Counting Principle allow repetitions? Yes, if each choice in a step can be repeated regardless of previous selections, the multiplication rule remains valid. If repetition is not allowed, the counts at each step must adjust accordingly.

What distinguishes the Multiplication Principle from the Addition Principle? The multiplication principle is used for sequences of independent choices (“AND” situations), while the addition principle is used when the options are disjoint (“OR” situations). Both can occur in compound counting scenarios and must be applied according to the logical structure of the problem.

For deeper insight into probability and related theorems utilizing the multiplication rule, visit Multiplication Theorem Of Probability.