Understanding the Graph of a Quadratic Polynomial

A quadratic polynomial in a single real variable is an algebraic expression of degree two, generally represented as $f(x) = a x^2 + b x + c$ where $a \neq 0$ and $a, b, c \in \mathbb{R}$. The graphical representation of such polynomials yields a curve known as a parabola, whose precise geometry and orientation are dictated by the values of $a$, $b$, and $c$.

Standard Formulation of the Quadratic Polynomial and Parabola Structure

Consider a quadratic polynomial $f(x) = a x^2 + b x + c$. The graph of $y = f(x)$ constitutes a parabola in the Cartesian plane. The coefficient $a$ dictates the direction in which the parabola opens. When $a > 0$, the parabola opens upwards, and when $a < 0$, the parabola opens downwards. If $a = 0$, the polynomial is not quadratic, and the resulting graph is linear.

The axis of symmetry of the parabola described by $y = a x^2 + b x + c$ is a vertical line. Its equation is given by $x = -\dfrac{b}{2a}$. This line passes through the vertex of the parabola, which is the extremal point on its curve. The coordinates of the vertex $(x_v, y_v)$ are found as follows:

Firstly, set $x_v = -\dfrac{b}{2a}$.

Then, calculate $y_v$ using $f(x_v)$:

$y_v = a(x_v)^2 + b x_v + c$

Substituting the value of $x_v$ gives

$y_v = a \left( -\dfrac{b}{2a} \right)^2 + b \left( -\dfrac{b}{2a} \right) + c$

Calculate the square:

$\left( -\dfrac{b}{2a} \right)^2 = \dfrac{b^2}{4 a^2}$

So, $y_v = a \cdot \dfrac{b^2}{4a^2} + b \cdot \left( -\dfrac{b}{2a} \right) + c$

$= \dfrac{a b^2}{4 a^2} - \dfrac{b^2}{2 a} + c$

$\dfrac{a b^2}{4 a^2}$ simplifies to $\dfrac{b^2}{4 a}$, thus:

$y_v = \dfrac{b^2}{4a} - \dfrac{b^2}{2a} + c$

To combine these fractions, use a common denominator:

$\dfrac{b^2}{4a} - \dfrac{2b^2}{4a} = -\dfrac{b^2}{4a}$

Therefore, $y_v = -\dfrac{b^2}{4a} + c$.

Alternatively, $y_v = f\left(-\dfrac{b}{2a}\right)$. The vertex is hence

$\left(-\dfrac{b}{2a}, \; c - \dfrac{b^2}{4a}\right)$.

X-Intercepts and Real Roots in the Parabolic Graph

The points at which the graph of $y = a x^2 + b x + c$ intersects the $x$-axis are the real roots (zeros) of the quadratic polynomial. These are obtained by solving $f(x) = 0$:

$a x^2 + b x + c = 0$

The discriminant $D$ is defined by $D = b^2 - 4 a c$.

There are three distinct possibilities, determined by the value of $D$:

$D > 0$: Two distinct real roots, parabola cuts the $x$-axis at two points.

$D = 0$: One real repeated root, parabola touches the $x$-axis at one point (vertex lies on the $x$-axis).

$D < 0$: No real roots, parabola does not intersect the $x$-axis.

The explicit formulas for the real roots (when they exist) are:

$x_1 = \dfrac{ -b + \sqrt{b^2 - 4ac} }{2a }, \quad x_2 = \dfrac{ -b - \sqrt{b^2 - 4ac} }{2a }$

For more detailed analysis of quadratic equations and their roots, refer to Quadratic Equations Roots.

Y-Intercept and Constant Term Interpretation

The $y$-intercept of the parabola is the point at which the curve meets the $y$-axis. This is found by setting $x = 0$ in $f(x)$, yielding the point $(0, c)$. The constant term $c$ is thus the $y$-coordinate of the intersection with the $y$-axis.

Significance of the Discriminant in Parabolic Geometry

The calculation and interpretation of the discriminant $D = b^2 - 4ac$ facilitates the prediction of the number and nature of $x$-intercepts of the parabola. Furthermore, it is employed in identifying the vertex's $y$-coordinate as $y_v = -\dfrac{D}{4a}$ using the previously derived relation for $y_v$.

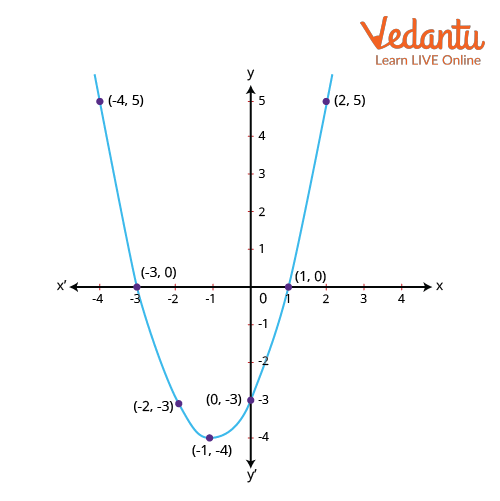
Worked Example: Precise Construction of a Quadratic Parabola

Given: $f(x) = x^2 + 2x - 3$

Here, $a = 1,\; b = 2,\; c = -3$.

1. Parabola Opening: Since $a = 1 > 0$, the parabola opens upwards.

2. Discriminant Calculation: $D = b^2 - 4 a c = 2^2 - 4 \cdot 1 \cdot (-3) = 4 + 12 = 16$.

3. Roots: Solve $x^2 + 2x - 3 = 0$.

Factorize: $x^2 + 2x - 3$

Write $-3$ as $+3 - 6$ to factor:

$x^2 + 2x - 3 = x^2 + 3x - x - 3 = x(x + 3) -1(x + 3) = (x + 3)(x - 1)$

Thus, $x = -3$ and $x = 1$

4. Vertex:

$x_v = -\dfrac{b}{2a} = -\dfrac{2}{2} = -1$

$y_v = f(-1) = (-1)^2 + 2(-1) - 3 = 1 - 2 - 3 = -4$

So, the vertex is at $(-1, -4)$.

5. $y$-intercept: Set $x = 0$: $f(0) = 0^2 + 2 \cdot 0 - 3 = -3$. Thus, the $y$-intercept is $(0, -3)$.

The points $(-3, 0)$ and $(1, 0)$ are the $x$-intercepts, while $(0, -3)$ is the $y$-intercept, and $(-1, -4)$ is the vertex.

For exploration of maximum and minimum values, see Max And Min Of Quadratic Polynomial.

Sum and Product of Zeros: Algebraic Connection to Coefficients

Let the zeros (roots) of $f(x) = a x^2 + b x + c$ be $\alpha$ and $\beta$. Using the quadratic factorization, we can write:

$f(x) = a(x - \alpha)(x - \beta)$

Expanding this product:

$= a\; (x^2 - (\alpha + \beta)x + \alpha\beta)$

$= a x^2 - a(\alpha + \beta)x + a \alpha\beta$

Comparing coefficients with $a x^2 + b x + c$, equate terms:

$-a(\alpha + \beta) = b$

$\implies \alpha + \beta = -\dfrac{b}{a}$

$a \alpha \beta = c$

$\implies \alpha \beta = \dfrac{c}{a}$

Result: The sum of the zeros of the quadratic polynomial is $-\dfrac{b}{a}$, and the product of the zeros is $\dfrac{c}{a}$.

For background on general polynomial functions, refer to Functions And Its Types.

Orientation of the Parabola and Role of the Leading Coefficient

The sign of the coefficient $a$ in $f(x) = a x^2 + b x + c$ is solely responsible for determining the direction in which the parabola opens. When $a > 0$, the arms of the parabola extend upwards, and for $a < 0$, they extend downwards. This attribute also determines whether the function possesses a minimum value (if $a>0$) or a maximum value (if $a<0$) at the vertex.

For visual reference, the graphical shape of a standard parabola corresponding to $a > 0$ is illustrated below.

Additional Interpretations: Special Cases

When the quadratic polynomial has a double root ($D = 0$), the vertex of the parabola coincides with the $x$-axis. When $D < 0$, both roots are non-real, and the parabola does not intersect the $x$-axis at any real point. These cases are directly reflected in the nature and placement of the graph.

In quadratic polynomials of the form $y^2 + py + q = 0$, with $y$ as the variable instead of $x$, the parabolic graph is oriented horizontally. The principles for calculation of roots, vertex, and intercepts remain analogous, though the variable roles are exchanged.

Summary of Structural Features in Quadratic Polynomial Graphs

The graph of a quadratic polynomial $y = a x^2 + b x + c$ is a parabola with symmetry about the vertical line $x = -\dfrac{b}{2a}$. The vertex is situated at $\left(-\dfrac{b}{2a},\; c - \dfrac{b^2}{4a}\right)$, and the $y$-intercept is $(0, c)$. Real roots of the polynomial, when present, are found using the quadratic formula. The nature of the parabola's $x$-intercepts is determined by the discriminant. The orientation is established by the sign of $a$. The relations $\alpha + \beta = -\dfrac{b}{a}$ and $\alpha\beta = \dfrac{c}{a}$ always hold for the zeros of the quadratic. For study of other standard graphs in JEE, refer to Graphs Of Sine And Cosine.

Further Study and Related Concepts

Comprehensive understanding of the graph of a quadratic polynomial enables deeper analysis of optimization, loci, and inequalities. Progression to limits and continuity can be pursued at Limit Continuity And Differentiability.