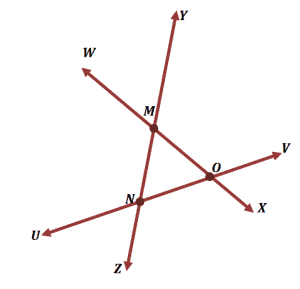
What Makes Intersecting Lines Different from Concurrent Lines?
In the world of geometry, lines play a pivotal role as fundamental building blocks and is important for JEE Main 2026. They serve as the foundation for various geometric concepts and are essential in understanding the relationships between different shapes and figures. Two primary types of lines that frequently appear in geometric discussions are intersecting lines and concurrent lines. While these terms may seem similar at first glance, they have distinct characteristics and implications. In this article, we will differentiate between intersecting lines and concurrent lines. Intersecting lines are two or more lines that cross paths at a particular point. This intersection forms what is known as an intersection point, where the lines meet. Concurrent lines, on the other hand, refer to three or more lines that intersect at a single common point. This point of intersection is called the concurrency point.
Table of Content
Intersecting lines refer to two or more lines that cross paths at a specific point, known as the intersection point.
Characteristics of Intersecting Lines
Intersection Point: It refers to the precise location where two or more lines meet or cross each other. This point is common to all intersecting lines and can be denoted as a single coordinate on a coordinate plane.
Angle Formation: The intersection of lines leads to the formation of angles. Depending on the angle formed, intersecting lines can be classified as acute (less than 90 degrees), right (exactly 90 degrees), or obtuse (greater than 90 degrees) angles.
Cross Pattern: Intersecting lines create a distinctive X-shaped pattern where they meet. This pattern allows for visual identification and differentiation of intersecting lines.
Parallel and Perpendicular Lines: If two lines intersect and form right angles (90 degrees) at the intersection point, they are called perpendicular lines. In contrast, lines that never intersect, regardless of their length, are called parallel lines.
Shape Creation: Intersecting lines are instrumental in constructing and understanding various geometric shapes. They contribute to the formation of polygons, including triangles, quadrilaterals, pentagons, and more, by connecting their vertices.
Transversal Intersections: When a line intersects two or more parallel lines, it is known as transversal. Transversals produce distinct angle relationships, such as corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.
Application in Geometry: Intersecting lines are foundational in geometry. They are crucial for understanding concepts such as angle relationships, the formation of polygons, and the identification of parallel and perpendicular lines.
Understanding intersecting lines is vital for comprehending the geometry of various shapes and figures. By recognizing their properties and significance, we can navigate the complex world of geometry with ease and clarity.
What is Concurrent Lines?
Concurrent lines refer to three or more lines that intersect at a single common point. This point of intersection is known as the concurrency point. Unlike intersecting lines, which can cross at various points, concurrent lines converge at one specific location.
Characteristics of Concurrent Lines
Concurrency Point: It is the unique point where three or more lines intersect. Unlike intersecting lines, which can intersect at various points, concurrent lines converge at one specific location. This concurrency point is common to all the lines involved.
Triangle Centers: Concurrent lines play a significant role in the study of triangles and their properties. Specifically, three important concurrent lines exist within a triangle:
Centroid: The centroid is the concurrency point of the medians of a triangle. The medians are lines drawn from each vertex to the midpoint of the opposite side. The centroid divides each median into segments with a ratio of 2:1.
Circumcenter: The circumcenter is the concurrency point of the perpendicular bisectors of a triangle. The perpendicular bisectors are lines that intersect at right angles and divide the sides of the triangle equally. The circumcenter is equidistant from the triangle's vertices.
Incenter: The incenter is the concurrency point of the angle bisectors of a triangle. The angle bisectors divide the interior angles of the triangle equally. The incenter is equidistant from the triangle's sides.
Circles and Tangents: Concurrent lines are also closely related to circles. For instance, the concurrent lines formed by the perpendicular bisectors of the sides of a triangle intersect at the circumcenter, which is the center of the triangle's circumcircle. Additionally, the tangents to a circle drawn from an external point are concurrent lines that intersect at the point of contact on the circle.
Balance and Equilibrium: The concurrency of lines in a triangle reflects a sense of balance and equilibrium. For example, the centroid, formed by the intersection of the medians, represents the center of mass of the triangle.
Practical Applications: Concurrent lines find applications in various fields. In architecture and engineering, the concept of concurrency is used for structural analysis, where forces or loads converge at a central point. In navigation, lines of latitude (parallels) and lines of longitude (meridians) are examples of concurrent lines that intersect at the Earth's poles.
Understanding the concept of concurrent lines and their associated concurrency points and triangle centers enhances our ability to analyze and appreciate the geometric properties of triangles and other figures. These lines offer valuable insights into the balance, symmetry, and stability found in both mathematical and real-world contexts.
Difference Between Intersecting Lines and Concurrent Lines
JEE Main Subject-wise Difference Between Topics
As you prepare for the JEE Main exam, it's crucial to understand the difference between topics in each subject. This table provides a concise overview of the key distinctions between various concepts in Physics, Chemistry, and Mathematics, helping you to uplift your study approach and maximise your preparation effectiveness.
Summary
From this article Concurrent Lines And Intersecting Lines, it can be concluded that intersecting lines involve the crossing of two or more lines at one or more points, while concurrent lines refer to three or more lines intersecting at a single point. Intersecting lines are primarily concerned with the points of intersection and the formation of angles, while concurrent lines emphasize the common point of intersection and its relationship with the lines.
JEE Main 2026 Subject-Wise Important Chapters
The JEE Main 2026 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.
Check Other Important Links for JEE Main 2026
JEE Main 2026 needs well-structured study materials. Here are some valuable resources to help you plan your preparation and practice efficiently.
FAQs on Understanding the Difference Between Intersecting and Concurrent Lines
1. What is the difference between intersecting lines and concurrent lines?
Intersecting lines are lines that cross at a single point, while concurrent lines are three or more lines that all meet at the same point.
Key differences:
- Intersecting lines involve only two lines meeting at one point.
- Concurrent lines include three or more lines passing through a common point called the point of concurrency.
- All concurrent lines are intersecting, but not all intersecting lines are concurrent.
2. Define intersecting lines with an example.
Intersecting lines are two lines that meet or cross each other at one common point.
Example:
- If line AB and line CD cross at point P, then AB and CD are intersecting lines.
- They form an angle at the point of intersection.
3. What are concurrent lines with an example?
Concurrent lines are three or more lines that all pass through a single point.
Example:
- If lines l, m, and n all meet at point O, they are concurrent lines, and O is their point of concurrency.
4. Can two lines be concurrent?
No, two lines that meet are called intersecting lines. The term concurrent lines specifically refers to three or more lines passing through a single point.
5. Is every set of intersecting lines also concurrent lines?
No, not every set of intersecting lines is concurrent. Two lines that intersect are just intersecting, while concurrent lines require at least three lines meeting at one point.
6. What is the point of concurrency?
Point of concurrency is the single point where three or more concurrent lines intersect.
Example:
- In a triangle, the medians meet at a point called the centroid — the point of concurrency.
7. How do you identify intersecting lines on a graph?
To identify intersecting lines on a graph, look for two lines that cross each other at exactly one point. Their point of intersection is where they meet on the graph.
8. List real-life examples of intersecting and concurrent lines.
Real-life examples:
- Intersecting lines: The crossing of two roads at a junction.
- Concurrent lines: The hands of a clock at 12 o'clock (all meet at the center, the point of concurrency).
9. Why are concurrent lines important in geometry?
Concurrent lines are important in geometry because they help locate special points like the centroid, incenter, circumcenter, and orthocenter of triangles. These points have important properties used in geometric constructions.
10. What are the properties of concurrent lines?
Properties of concurrent lines:
- Three or more lines meet at a single point (point of concurrency).
- The point is unique for a given set of lines.
- Concurrent lines are used to define important geometric locations in triangles and other figures.
11. Can parallel lines be concurrent or intersecting?
No, parallel lines are neither intersecting nor concurrent because they never meet at any point, no matter how far they are extended.
12. How do you prove that three lines are concurrent?
To prove that three lines are concurrent, show that they all pass through a common point.
Steps:
- Find the intersection of two lines first.
- Check if the third line passes through that intersection point.
- If all three go through the same point, the lines are concurrent.
