




Key Rules and Examples of Mathematical Inequalities
Inequalities are foundational in algebra, analysis, and mathematical reasoning as they provide a precise method to compare real numbers, algebraic expressions, and functions. An inequality asserts that one mathematical quantity is greater than, less than, or otherwise unequal to another, using specific relational symbols.
Formal Structure and Symbols for Mathematical Inequalities
Let $a$ and $b$ be real numbers. The symbols $>$, $<$, $\geq$, $\leq$, and $\neq$ are used to compare $a$ and $b$ as follows:
Strict Inequality: $a > b$ means $a$ is strictly greater than $b$; $a < b$ means $a$ is strictly less than $b$.
Non-Strict (Weak) Inequality: $a \geq b$ means $a$ is greater than or equal to $b$; $a \leq b$ means $a$ is less than or equal to $b$.
Inequality of Distinctness: $a \neq b$ means $a$ and $b$ are not equal.
Classification: Linear and Non-Linear Inequalities
Linear Inequality in One Variable: An inequality of the form $ax + b \gt 0$, $ax + b \geq 0$, $ax + b \lt 0$, or $ax + b \leq 0$, where $a$, $b$ are real constants and $a \neq 0$, is called a linear inequality in one variable.
Linear Inequality in Two Variables: An inequality of the form $ax + by + c \gt 0$ or similar, where $a$, $b$, $c \in \mathbb{R}$ and at least one of $a$, $b$ is non-zero, is called a linear inequality in two variables.
Non-linear inequalities involve degrees greater than one, or more complex structures, such as quadratic or rational inequalities.
Addition and Subtraction Properties of Inequalities
Addition Property: If $a \gt b$ and $c$ is any real number, then $a + c \gt b + c$. This property also holds for the symbols $\geq$, $<$, and $\leq$ analogously.
Proof: Given $a > b$, by the definition of the order relation in $\mathbb{R}$, adding the same real number $c$ to both sides preserves the inequality: $a + c > b + c$.
Subtraction Property: If $a > b$ and $c$ is any real number, then $a - c \gt b - c$.
This follows as $a - c = a + (-c)$ and $b - c = b + (-c)$. Then by the addition property, $a + (-c) > b + (-c)$.
Multiplicative and Divisional Properties for Inequalities
Multiplication by Positive Numbers: If $a > b$ and $k > 0$, then $ak > bk$. The sense of the inequality is preserved.
Proof: Since $k > 0$, multiplying each side of $a > b$ by $k$ gives $a \cdot k \gt b \cdot k$.
Multiplication by Negative Numbers: If $a > b$ and $k < 0$, then $ak < bk$, so the sense of the inequality is reversed.
Proof: Let $k = -|k| < 0$. Multiplying both sides by $k$ reverses the inequality: $a \cdot k < b \cdot k$.
Division by Non-Zero Numbers: If $a > b$ and $k > 0$, then $\dfrac{a}{k} \gt \dfrac{b}{k}$. If $k < 0$, then $\dfrac{a}{k} \lt \dfrac{b}{k}$.
Transitive and Converse Properties of Inequalities
Transitive Property: For real numbers $a$, $b$, $c$, if $a \geq b$ and $b \geq c$, then $a \geq c$. If at least one inequality is strict, then $a \gt c$.
Converse (Reverse) Property: If $a \gt b$, then $b \lt a$. More generally, the direction of an inequality is reversed if the order of the terms is reversed.
Solving Linear Inequality in One Variable: Stepwise Method
Consider the inequality $2x + 5 < 4x - 15$. Each algebraic transformation must preserve the inequality.
Step 1: Subtract $2x$ from both sides.
$2x + 5 - 2x < 4x - 15 - 2x$
$5 < 2x - 15$
Step 2: Add $15$ to both sides.
$5 + 15 < 2x - 15 + 15$
$20 < 2x$
Step 3: Divide both sides by $2$ (a positive number).
$\dfrac{20}{2} < \dfrac{2x}{2}$
$10 < x$
Result: $x > 10$.
Solving Linear Inequality with Fractions: Worked Example
Given: $\dfrac{y-3}{2} \geq \dfrac{5}{4}$
Step 1: Multiply both sides by $4$. $4 > 0$ retains the direction.
$4 \cdot \dfrac{y-3}{2} \geq 4 \cdot \dfrac{5}{4}$
$2(y-3) \geq 5$
Step 2: Expand the left side: $2y - 6 \geq 5$
Step 3: Add $6$ to both sides.
$2y - 6 + 6 \geq 5 + 6$
$2y \geq 11$
Step 4: Divide both sides by $2$.
$\dfrac{2y}{2} \geq \dfrac{11}{2}$
$y \geq 5.5$
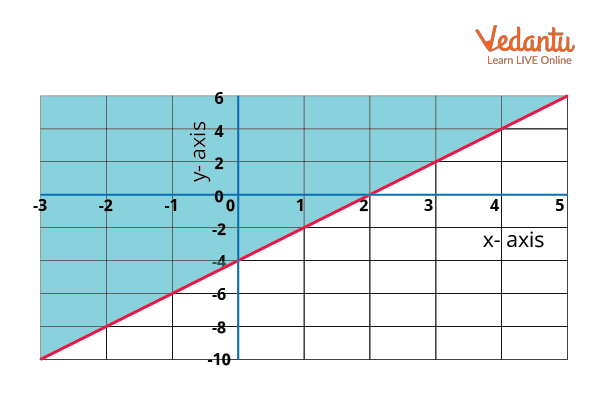
Graphical Representation of Linear Inequalities in Two Variables
Let $2y \geq 4x - 8$. First, isolate $y$:
$2y \geq 4x - 8$
Divide both sides by $2$:
$\dfrac{2y}{2} \geq \dfrac{4x-8}{2}$
$y \geq 2x - 4$
The boundary is the straight line $y = 2x - 4$. The solution set for $y \geq 2x - 4$ consists of all points in the coordinate plane that lie on or above this line. For detailed methodology on graphing inequalities, see Understanding Sets, Relations, And Functions.
Case Distinction: Inequality Involving Multiplication and Division by Negatives
When both sides of an inequality are multiplied or divided by a negative number, the direction must be reversed. Consider the inequality $x - 5 > 3$.
Step 1: Subtract $x$ from both sides: $x - x - 5 > 3 - x$ yields $-5 > 3 - x$.
Step 2: Subtract $3$ from both sides: $-5 - 3 > 3 - x - 3$ yields $-8 > -x$.
Step 3: Multiply both sides by $-1$ ($-1 < 0$) and reverse the direction:
$(-8) \cdot (-1) < (-x) \cdot (-1)$ yields $8 < x$.
Result: $x > 8$.
Logical Combination and Transitivity in Chains of Inequalities
Given a chain $a > b \geq c > d$, one can deduce $a > d$ by transitivity. However, if any link is non-strict ($\geq$), then the final relation is non-strict unless all intermediate relations are strict.
For details on induction in inequalities, refer to Understanding Mathematical Induction.
Worked Example: Deduction from a Chain of Inequalities
Given: $h < a < t = g > u \geq v \geq b$. Determine whether $t > b$ and $g > h$ are true.
$t = g \gt u \geq v \geq b$. Since $t = g$, and $g \gt u \geq v \geq b$, $t \gt b$.
Also, $h < a < t = g$. Therefore, $h < a < t$ and $t = g \implies h < g$, so $g > h$.
Result: Both $t > b$ and $g > h$ are definitely true.
Further Reading: Advanced Inequalities and Olympiad Concepts
Beyond linear inequalities, the study extends to quadratic, polynomial, rational, and classical inequalities such as the Cauchy-Schwarz, AM-GM, and triangle inequalities.
FAQs on Understanding the Basics of Inequalities
1. What are the basics of inequalities in mathematics?
Basics of inequalities refer to the fundamental rules and properties used to compare the relative sizes of numbers or algebraic expressions.
- An inequality compares two values and shows if one is greater, smaller, or not equal to the other.
- The main inequality symbols are > (greater than), < (less than), ≥ (greater than or equal to), ≤ (less than or equal to), and ≠ (not equal to).
- Common operations include adding, subtracting, multiplying, or dividing both sides by the same number, with special attention to sign changes for negative values.
2. What are the main types of inequalities?
Inequalities in mathematics can be categorised into several main types.
- Linear Inequalities: Expressions of the form ax + b > c.
- Quadratic Inequalities: Inequalities involving terms up to x2.
- Double Inequalities: Those that express a value between two bounds, e.g., a < x < b.
- Compound Inequalities: Combinations of two or more inequalities connected by 'and' or 'or'.
3. What are the rules for solving inequalities?
Solving inequalities follows specific rules similar to equations, with a key difference when multiplying or dividing by negative numbers.
- You can add or subtract the same value on both sides without changing the inequality sign.
- You can multiply or divide both sides by a positive number; the sign remains the same.
- Multiplying or dividing both sides by a negative number reverses the direction of the inequality sign.
4. How do you represent inequalities on a number line?
Inequalities are represented on a number line by showing all values that satisfy the given condition.
- A filled circle is used for inclusive inequalities (≥ or ≤), and an open circle for strict inequalities (< or >).
- The line to the right or left of the circle indicates the direction of the solutions.
5. When do you reverse the inequality sign while solving?
The inequality sign is reversed when you multiply or divide both sides of an inequality by a negative number.
- This is a crucial property and is frequently tested in exams.
- For example, if -2x < 6, dividing both sides by -2 changes the sign: x > -3.
6. Can you give an example of solving a simple linear inequality?
A basic example of a linear inequality is: Solve 2x + 5 > 9.
- First, subtract 5 from both sides: 2x > 4.
- Then, divide both sides by 2: x > 2.
7. What are the common mistakes students make while solving inequalities?
Students often make errors in inequality questions by forgetting to reverse the sign when multiplying or dividing by negatives and by mishandling brackets.
- Neglecting to change the sign after multiplying/dividing by a negative.
- Incorrectly simplifying expressions on both sides.
- Misrepresenting solutions on a number line.
8. How can inequalities be applied in real-life situations?
Inequalities are used in many real-life contexts to set limits, boundaries, or conditions.
- Banking: Limits on withdrawals (e.g., amount ≤ Rs. 10,000).
- Age restrictions: For voting or contests (age ≥ 18).
- Budgeting: Ensuring spend does not exceed income.
9. What is the difference between an equation and an inequality?
The key difference is that an equation shows two expressions are equal, while an inequality shows a greater than, less than, or not equal relationship.
- Equations use the = sign, and have a unique solution or specific set of solutions.
- Inequalities use >, <, ≥, ≤, or ≠, with solutions often in the form of intervals.
10. Can quadratic inequalities have more than one solution?
Yes, quadratic inequalities may result in a range or interval of solutions rather than a single value.
- For example, solving x2 < 9 gives -3 < x < 3.
- The solution set can be expressed as an interval and represented graphically.


































