Question

Let the latus rectum of the parabola \[{y^2} = 4x\] be the common chord to the circle \[{C_{1{\rm{ }}}}\] and \[{{\rm{C}}_2}\] each of them having radius \[2\sqrt 5 \]. Then the distance between the centers of the circle \[{C_{1{\rm{ }}}}\] and \[{{\rm{C}}_2}\]is,
A.8
B.\[8\sqrt 5 \]
C.\[4\sqrt 5 \]
D.12

Answer 1

Hint: First draw the diagram of the stated problem, from the diagram we can say that \[{C_1}B = B{C_2}\] as B is the middle point of the line \[{C_1}{C_2}\], therefore we can conclude that \[{C_1}{C_2} = 2{C_1}B = 2B{C_2}\] . Now, apply the Pythagoras theorem to obtain the value of \[{C_1}B\]. Multiply the obtained value of \[{C_1}B\] by 2, to obtain the required value.

Formula used:
Pythagoras theorem states that, for a right-angle triangle \[{\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {height} \right)^2}\] .

Complete step by step solution:
For the given parabola the latus rectum is 4 as in the general form \[{y^2} = 4ax\] the latus rectum is 4a.
So, the diagram of the stated problem is,

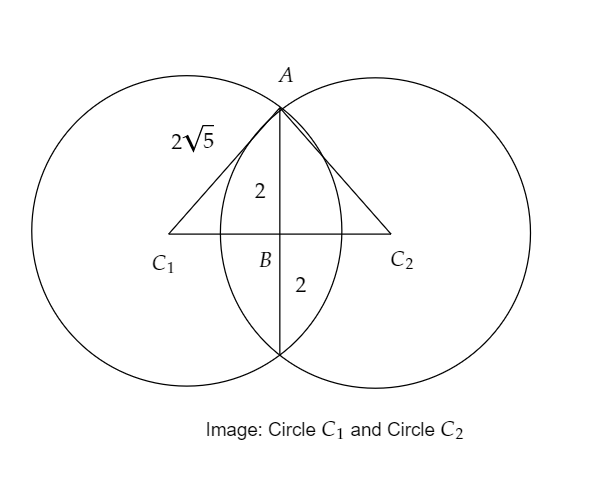
The given two circles have an equal radius, and it is given that the common chord of these two circles is the latus rectum of the parabola \[{y^2} = 4x\], here the length of latus rectum is 4 so, length of AB must be half of the length of the latus rectum. As the latus rectum divides the line \[{C_1}{C_2}\] into two equal parts so we can conclude that \[{C_1}{C_2} = 2{C_1}B = 2B{C_2}\] .
Now, it is a right-angle triangle.
Apply Pythagoras theorem on this triangle to obtain the value of the base.
\[{\left( {A{C_1}} \right)^2} = {\left( {{C_1}B} \right)^2} + {\left( {BA} \right)^2}\]
\[ \Rightarrow {\left( {2\sqrt 5 } \right)^2} = {\left( {{C_1}B} \right)^2} + {\left( 2 \right)^2}\]
\[ \Rightarrow 4 \times 5 = {\left( {{C_1}B} \right)^2} + 4\]
\[\begin{array}{l} \Rightarrow {\left( {{C_1}B} \right)^2} = 20 - 4\\{\rm{ = 16}}\end{array}\]
Therefore, \[{C_1}B = \pm 4\]
As the distance can-not be negative therefore \[{C_1}B = 4\]
Hence,
 \[\begin{array}{c}{C_1}{C_2} = 2{C_1}B\\ = 2 \times 4\\ = 8\end{array}\]
Hence the Required value is 8.

Note: Students are often confused to calculate the latus rectum of a parabola. They do not take 4a as the latus rectum. They calculate the latus rectum as 1. But the correct latus rectum is 4.