Question

Let S be the set of all real roots of the equation ${3^x}({3^x} - 1) + 2 = |{3^x} - 1| + |{3^x} - 2|$ Then S is
A. is a singleton
B. is an empty set.
C. contains at least four elements
D. contains exactly two elements.

Answer 1

Hint: In this type of question, we will be using the concept of the modulus function. First, we will assume ${3^x}$some variable then we will be drawing the graph of the equation formed. After getting the graph of the LHS equation and RHS equation we can see at how many points they are cutting each other.

Complete step by step Solution:
The modulus function only gives a positive value of any number as the output. It is also known as the absolute value function because it gives a non-negative value for any independent quantity.
It does not matter what's inside the function( if it is positive or negative)
In other words, a modulus function gives only the magnitude of a number

It is commonly represented as $y = |x|$, where x represents a real number, and $y = f(x)$, representing all positive real numbers, including 0,

Then a modulus can be defined is given below:
\[f(x) =\begin{cases}x \\-x\end{cases}\]
Here, where x is any non-negative number, the function generates a positive equivalent of x. For a negative number, the function generates (−x) were −(−x) = which is the positive value of x.
Now let say assume ${3^x} = t$
$t(t - 1) + 2 = |t - 1| + |t - 2|$
$ \Rightarrow {t^2} - t + 2 = |t - 1| + |t - 2|$
We will be plotting the graph of both the LHS function and RHS function

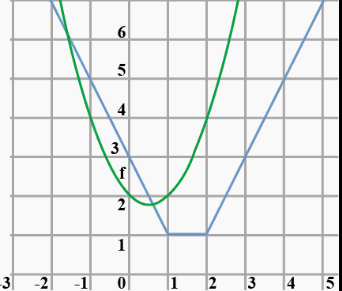
As ${3^x}$ is always positive, therefore only positive values of t will be the solution.
Hence, we have only one solution.

Hence, the correct option is A.

Note:We should keep it in the domain of the modulus function. It always gives a positive value so the graphical representation of the modulus function is always above the x-axis. Care should be taken while taking the negative or positive value of x. In our question, it is always positive.