
Let \[L\] denote the set of all straight lines in a plane. Let a relation \[R\] be defined by \[\alpha R\beta \Leftrightarrow \alpha \bot \beta \],\[\alpha ,\beta \in L\]. Then \[R\] is
A. Reflexive
B. Symmetric
C. Transitive
D. None of these
Answer
217.8k+ views
Hint: In this question, we are given a relation \[R\] which is defined as \[\alpha R\beta \Leftrightarrow \alpha \bot \beta \],\[\alpha ,\beta \in L\]. We have to tell about what is the relation \[R\], is reflexive or symmetric, or it is transitive or it is none of the mentioned properties. We will be using the definition and concept of reflexive, symmetric, and transitive to find out.
Complete step-by-step solution:
From the definitions of reflexive, symmetric, and transitive, we get the following results
1. Reflexive: As per the reflexive property, if \[R\] is reflexive then each line in the set \[L\] must be perpendicular to itself but this is not possible i.e., it is not possible that a line is perpendicular to itself
Thus, \[R\] is not reflexive
2. Symmetric: As per the symmetric property, if \[R\] is symmetric then a line in the set \[L\] must be perpendicular to another line and so the other line would also be perpendicular to the previous line i.e.,
If \[\alpha \bot \beta \Leftrightarrow \beta \bot \alpha \] which is true for all the lines present in the set \[L\].
3. Transitive: As per the transitive property, if \[R\] is transitive, \[l,m,n\] are 3 lines in the set \[L\], if \[l \bot m\] and \[m \bot n\], then \[l \bot n\] but this is not true in all cases.
Consider following example where \[l \bot m\] and \[m \bot n\] but \[l,n\] are not perpendicular.
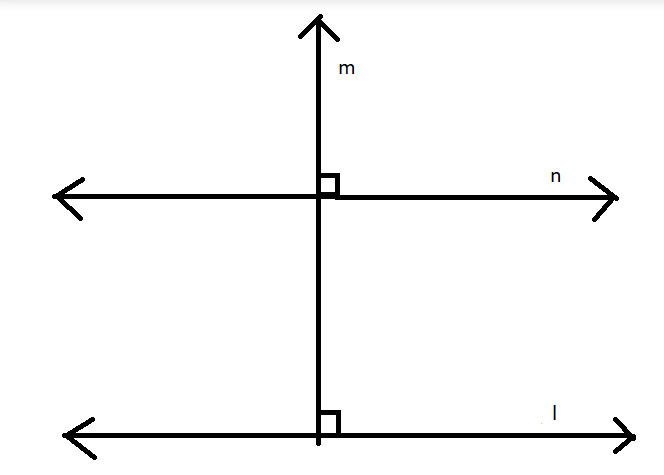
Image: figure shows 2 parallel lines \[l,n\] and \[m\] is perpendicular to \[l,n\].
So in all cases, if \[l \bot m\] and \[m \bot n\], then \[l \bot n\], this is not true.
Thus \[R\] is not transitive.
Hence, option (B) is correct
Note: While checking the transitive portion, the scholars might make the mistake of thinking of the matching axis with \[x\]-axis, \[y\]- axis, and \[z\]- axis in which all the axes are vertical to each other. But always flashback that to prove commodity is true, you have to give a perfect explanation not an illustration and to prove commodity wrong, we just need an illustration to do so.
Complete step-by-step solution:
From the definitions of reflexive, symmetric, and transitive, we get the following results
1. Reflexive: As per the reflexive property, if \[R\] is reflexive then each line in the set \[L\] must be perpendicular to itself but this is not possible i.e., it is not possible that a line is perpendicular to itself
Thus, \[R\] is not reflexive
2. Symmetric: As per the symmetric property, if \[R\] is symmetric then a line in the set \[L\] must be perpendicular to another line and so the other line would also be perpendicular to the previous line i.e.,
If \[\alpha \bot \beta \Leftrightarrow \beta \bot \alpha \] which is true for all the lines present in the set \[L\].
3. Transitive: As per the transitive property, if \[R\] is transitive, \[l,m,n\] are 3 lines in the set \[L\], if \[l \bot m\] and \[m \bot n\], then \[l \bot n\] but this is not true in all cases.
Consider following example where \[l \bot m\] and \[m \bot n\] but \[l,n\] are not perpendicular.

Image: figure shows 2 parallel lines \[l,n\] and \[m\] is perpendicular to \[l,n\].
So in all cases, if \[l \bot m\] and \[m \bot n\], then \[l \bot n\], this is not true.
Thus \[R\] is not transitive.
Hence, option (B) is correct
Note: While checking the transitive portion, the scholars might make the mistake of thinking of the matching axis with \[x\]-axis, \[y\]- axis, and \[z\]- axis in which all the axes are vertical to each other. But always flashback that to prove commodity is true, you have to give a perfect explanation not an illustration and to prove commodity wrong, we just need an illustration to do so.
Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




