Question

In Young's double slit experiment, in an interference pattern second minimum is observed exactly in front of one slit. The distance between the two coherent sources is ′d′ and the distance between source and screen is ′D′. The wavelength of light source used is :
(A) $\dfrac{{{d^2}}}{D}$
(B) $\dfrac{{{d^2}}}{{2D}}$
(C) $\dfrac{{{d^2}}}{{3D}}$
(D) $\dfrac{{{d^2}}}{{4D}}$

Answer 1

Hint: As this is the case of young double slit experiment and minima is formed so the condition of minima is used in the required formula of the path difference i.e. $Y = \left( {n + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{d}$, Y is the position of second minima in front of one slit i.e. $Y = \dfrac{d}{2}$, here n is order of fringe and for second minima n=1, then substitute the values and we will get the value of wavelength.

Diagram:
                       

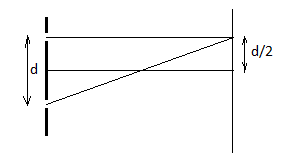
Complete step by step solution:
Minima is produced when the crust of one wave falls on the trough of another wave. Here, a second minima is produced in front of one slit so we use the condition of dark fringes.
The position of second minima just in front of one slit $Y = \dfrac{d}{2}$
The formula for minima is $Y = \left( {n + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{d}$…………………………(1)
Where, λ is the wavelength of light used
D is the distance of screen from the slit
D isn the distance between the slits
n is the order of fringes
For second minimum n=1 then put these values in equation (1) we get,
⇒ $\dfrac{d}{2} = \left( {1 + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{d} = \dfrac{{3\lambda D}}{{2d}}$
⇒ $\lambda = \dfrac{{2{d^2}}}{{6D}} = \dfrac{{{d^2}}}{{3D}}$

This the required value of wavelength used. Hence, C option is correct.

Note: As here we are talking about the second minima so just remember that for second minima n is equal to 1. And we must use the correct formula that the position of the fringe is equal to the odd multiple of fringe width. i.e. $Y = \left( {n + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{d}$, where $\dfrac{{\lambda D}}{d}$ is the fringe width which is the distance between the two crust and trough.