Question

In the loops shown, all curved sections are either semicircles or quarter circles. All the loops carry the same current. The magnetic fields at the centres have magnitudes ${B_1},\,{B_2},\,{B_3}$ and ${B_4}$: Assume the current to be in clockwise direction in the semicircle of radius $a$.

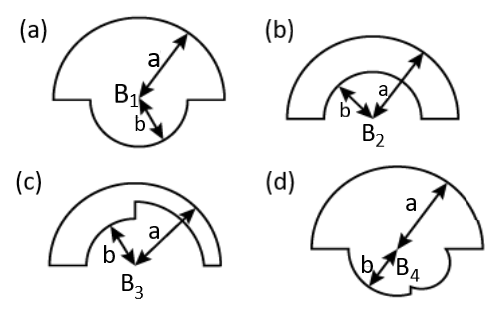
A. ${B_4}$is maximum
B. ${B_3}$ is minimum
C. ${B_4} > {B_1} > {B_2} > {B_3}$
D. ${B_1} > {B_4} > {B_3} > {B_2}$

Answer 1

Hint:A magnetic field can be visualised as a grid of various sets, each of which can be shown as a vector field. Field lines can also be used as a method. The lines connecting the collection of vectors. Additionally, the magnetic field lines are unbroken and never come to an end.

Complete step by step solution:
We have given the curved parts in the question as either semicircles or quarters. And their magnetic fields at the centre that have magnitudes ${B_1},\,{B_2},\,{B_3}$ and ${B_4}$. For ${B_1}$ and ${B_4}$ the contribution due to the different sections add up. And for ${B_2}$ and ${B_3}$, the contribution due to the outer sections opposes the contribution due to the inner sections.


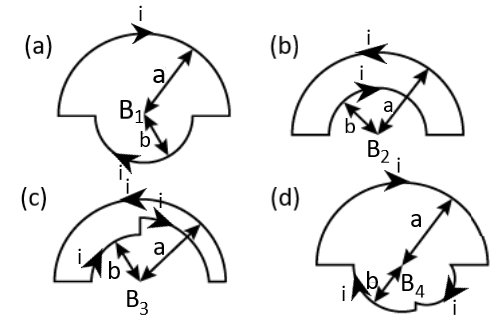
From the above figures, the equation for ${B_1}$can be represented as:
${B_1} = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{a} + \dfrac{1}{b}) = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{a} + \dfrac{1}{{2b}} + \dfrac{1}{{2b}}) \\ $
Similarly, the equations of the other sections are:
${B_2} = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{b} - \dfrac{1}{a}) = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{{2b}} + \dfrac{1}{{2b}} - \dfrac{1}{a}) \\$
$\Rightarrow {B_3} = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{{2b}} + \dfrac{1}{{2c}} - \dfrac{1}{a}) \\$
$\therefore {B_4} = \dfrac{{{\mu _0}i}}{4}(\dfrac{1}{a} + \dfrac{1}{{2b}} + \dfrac{1}{{2d}}) \\$
Thus, the section${B_1}$ and ${B_4}$ are greater than ${B_2}$ and ${B_3}$ for ${B_4}$, there is a section with a radius greater than $b$ and hence, it contributes more than the semi-circular section of a radius $b$ for ${B_1}$. Thus, ${B_4} > {B_1}$.

For ${B_3}$ there is a section with radius $ > b$ and hence it contributes less than the semi-circular section of radius $b$ for ${B_2}$. Thus, ${B_3} < {B_2}$. Therefore, ${B_4} > {B_1} > {B_2} > {B_3}$

Hence, the correct options are: (A), (B) and (C).

Note: As we know that the net charge through any section of any conductor is zero if a current flows through it. As a result, there is no electric field in the area around the conductor. The magnetic field will be zero near the axis of the cylindrical wire, as shown by the Biot and Savart law. Electric field along the axis of the wire must not be zero in order for current to flow through the wire.