Question

In the figure the ammeter ${A_1}$ reads a current of 10mA, while the voltmeter reads a potential difference of 3V. What does ammeter ${A_2}$ in mA read? The ammeters are identical, the internal resistance of the battery is negligible. (Consider all ammeters and voltmeters as non-ideal.)

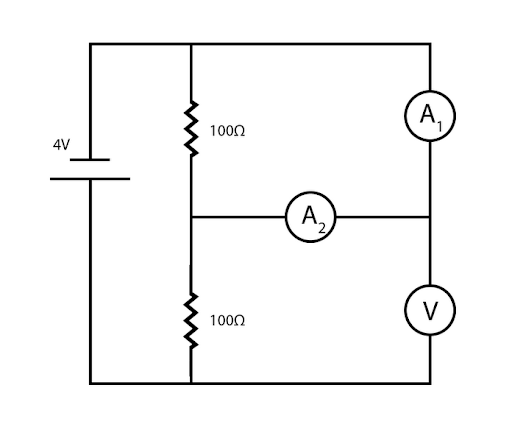
A. 6.67 mA
B. 3.12 mA
C. 1.12 mA
D. 5.14 mA

Answer 1

Hint:This question is from the current electricity section of physics. We need to apply Kirchhoff's laws to solve this problem. Using Kirchhoff's first law in the circuit, we can solve the numerical problem.

Complete step by step solution:
The voltage drop across the voltmeter is 3V. The emf is 4V. So the voltage across the ammeter ${A_1}$ is 1V. The resistance of the two ammeters will be $100\Omega $.
Taking x = potential of the point of intersection of the $100\Omega $ resistances and${A_2}$

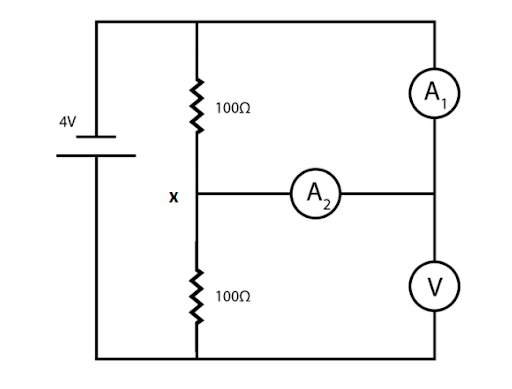
By applying Kirchhoff's first law, we will get.
$\dfrac{{x - 4}}{{100}} + \dfrac{x}{{100}} + \dfrac{{x - 1}}{{100}} = 0$
$\Rightarrow 3x = 5$
$\Rightarrow x = \dfrac{5}{3}$
Substitute the value of x to find the current in the ammeter ${A_2}$.
${A_2} = \dfrac{{x - 1}}{{100}} \\
\Rightarrow {A_2} = \dfrac{{\dfrac{5}{3} - 1}}{{100}} \\
\Rightarrow {A_2} = \dfrac{2}{{300}} \\
\Rightarrow {A_2} = 6.67 \times {10^{ - 3}}A \\ $
$\therefore {A_2} = 6.67\,mA$

Hence, the correct option is option A.

Additional Information: Two equalities known as Kirchhoff's circuit laws deal with the current and potential differences in electrical circuits. German physicist Gustav Kirchhoff came up with it in 1845. Currents at a circuit junction are governed by Kirchhoff's first law. It says that at a junction in an electrical circuit, the total amount of currents going in and out of the junction are equal. According to Kirchhoff's second law, the voltages across the elements in a circuit add up to zero if you loop in the circuit. This law is also called the voltage rule or the loop theorem.

Note: To apply Kirchhoff’s Voltage Law in this circuit, the following steps are needed: (1) Calculate the circuit's overall resistance (2) the circuit's overall current (3) the current flowing through each resistor (4) the voltage drop across each resistor