Question

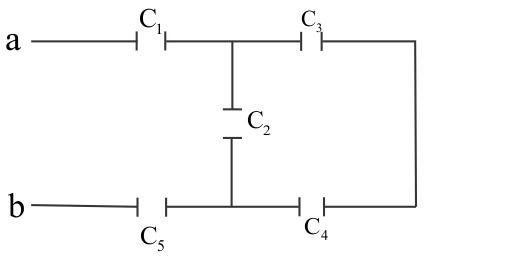
- In the figure, ${C_1} = {C_5} = 8.4\mu F$ and ${C_2} = {C_3} = {C_4} = 4.2\mu F$. The applied potential is ${V_{ab}} = 220V$. The equivalent capacitance of the network between points $a$ and $b$ is $C$. Calculate the value of $2C$.

Answer 1

Hint: The equivalent capacitance in the circuit when capacitors are parallel to each other is calculated by –
${C_{eq}} = {C_1} + {C_2} + \ldots {C_n}$
And the equivalent capacitance in the circuit when capacitors are in series with each other is calculated by –
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \ldots + \dfrac{1}{{{C_n}}}\]
where, $n$ is the number capacitors.
Then, find the equivalent capacitance and multiply it by $2$.

Complete step by step solution:
The circuit which has two or more electrical devices connected with it, then, there are many other ways by which we can connect them. They can either be series or parallel.
The circuit is said to be in series when two components in the circuit have a common node and the current which flows through all the components in the circuit is the same. In these types of circuits, there is only one path for the current. When the capacitors are connected in series, the equivalent capacitance is less than any one of the series capacitor’s individual response. The equivalent capacitance in series can be calculated by –
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \ldots + \dfrac{1}{{{C_n}}}\]
The circuit is said to be parallel when there are multiple paths for the current to flow. In this type of circuit, all components have the same voltage across all ends. The equivalent capacitance in parallel can be calculated by –
${C_{eq}} = {C_1} + {C_2} + \ldots {C_n}$
Now, according to the question, it is given that –
${C_1} = {C_5} = 8.4\mu F$
${C_2} = {C_3} = {C_4} = 4.2\mu F$
${V_{ab}} = 220V$
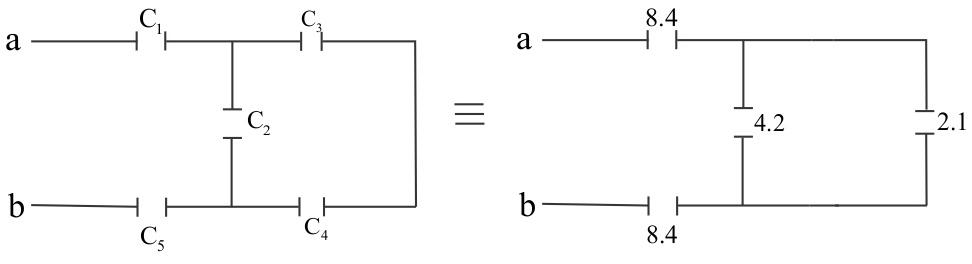
Now, the equivalent capacitance between ${C_3}$ and ${C_4}$ are in series, so the equivalent capacitance is –
$\dfrac{1}{{{C_{34}}}} = \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}$
Putting the values in above formula –
$
  \dfrac{1}{{{C_{34}}}} = \dfrac{1}{{4.2}} + \dfrac{1}{{4.2}} \\
  \dfrac{1}{{{C_{34}}}} = \dfrac{2}{{4.2}} \\
  {C_{34}} = 2.1\mu F \\
 $
So, the circuit can be drawn as –

The capacitors $4.2$ and $2.1$ are parallel to each other so, the equivalent capacitance is –
$
  {C_{234}} = 4.2 + 2.1 \\
  {C_{234}} = 6.3\mu F \\
 $

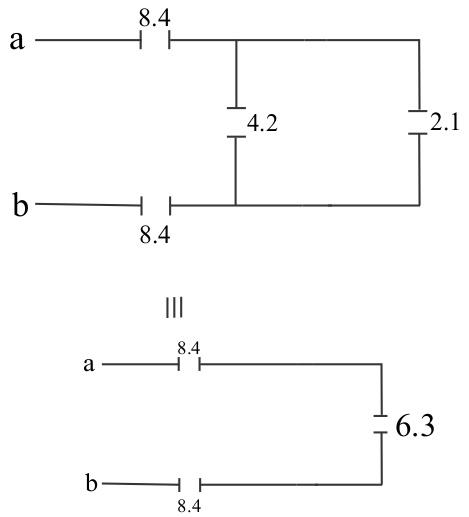
Now, the equivalent capacitance can be calculated by –
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{3.4}} + \dfrac{1}{{8.4}} + \dfrac{1}{{6.3}}$
By further solving, we get –
${C_{eq}} = 2.52\mu F$
To calculate $2C$ we have to multiply the equivalent capacitance by $2$, we get –
$2{C_{eq}} = 2 \times 2.52 = 5.04\mu F$

Hence, the value of $2C$ in the circuit is $5.04\mu F$.

Note: When the capacitors are connected in series, the equivalent capacitance is less than any one of the series capacitor’s individual response. When the capacitors are in parallel with each other, then, the overall effect is that of a single equivalent capacitor having the sum total of the plate areas of the individual capacitors.