Question

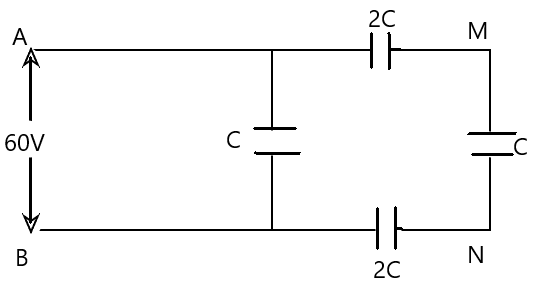
In the circuit shown, a potential difference of $60V$is applied across $AB$. The potential difference between the points $M$ and $N$ is:

A) $60V$
B) $15V$
C) $20V$
D) $30V$

Answer 1

Hint: The charges on the capacitors in series are the same. The electric potential across the capacitors or the combination of the capacitors in parallel are the same.

Complete step by step solution:

When capacitors are in series then the equivalent capacitance can be calculated as,
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}+\cdots \cdots +\dfrac{1}{{{C}_{n}}}$
Here, ${{C}_{1}},{{C}_{2}},{{C}_{3}}\ldots \ldots {{C}_{n}}$ are the capacitances of the capacitors connected in series, and ${{C}_{eq}}$is the equivalent value of the capacitance.

When capacitors are in series then the equivalent capacitance can be calculated as,
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}+\cdots \cdots +\dfrac{1}{{{C}_{n}}}$
Here, ${{C}_{1}},{{C}_{2}},{{C}_{3}}\ldots \ldots {{C}_{n}}$ are the capacitances of the capacitors connected in parallel, and ${{C}_{eq}}$ is the equivalent value of the capacitance.
From the electric circuit given, the capacitors in the right branch are in series.
Let equivalent capacitance of the capacitors in the right branch is ${{C}_{1}}$
Using the formula of the equivalent capacitance in series,
$\begin{array}{*{35}{l}}
{} & \dfrac{1}{{{C}_{1}}}=\dfrac{1}{2C}+\dfrac{1}{C}+\dfrac{1}{2C} \\
{} & \Rightarrow \dfrac{1}{{{C}_{1}}}=\dfrac{1+2+1}{2C} \\
{} & \Rightarrow \dfrac{1}{{{C}_{1}}}=\dfrac{4}{2C} \\
{} & \Rightarrow {{C}_{1}}=\dfrac{2C}{4} \\
{} & \therefore {{C}_{1}}=\dfrac{C}{2}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } \\
\end{array}$
Now, ${{C}_{1}}$ is in parallel with the capacitor on the left branch.
Let ${{C}_{eq}}$ is the equivalent capacitance of the given circuit.
Using the equivalent capacitance in parallel combination,
$\begin{array}{*{20}{l}}
{}&{{C_{eq}} = {C_1} + C} \\
{}&{ \Rightarrow {C_{eq}} = \dfrac{C}{2} + C} \\
{}&{ \Rightarrow {C_{eq}} = \dfrac{{C + 2C}}{2}} \\
{}&{\therefore {C_{eq}} = \dfrac{{3C}}{2}{\text{ }}\;{\text{ }}\;{\text{ }}}
\end{array}$
The equivalent capacitance of the given electric circuit is $\dfrac{3C}{2}$
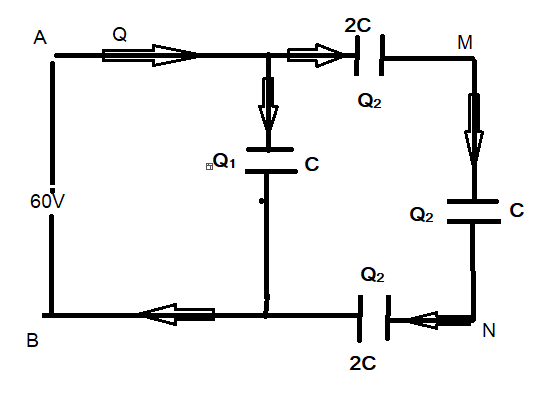
Let $Q$ is the total charge flown from the battery connected.
$\begin{array}{*{35}{l}}
{} & Q={{C}_{eq}}V \\
{} & \Rightarrow Q=\left( \dfrac{3C}{2} \right)\left( 60V \right) \\
{} & \therefore Q=90CV\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } \\
\end{array}$
The total charge gets distributed between the two branches.
${{Q}_{1}}+{{Q}_{2}}=Q\ldots \ldots \left( i \right)$
As right and the left branches are in parallel, so the electrical potential across both must be the same.
$\begin{array}{*{35}{l}}
{} & {{V}_{1}}={{V}_{2}} \\
{} & \Rightarrow \dfrac{{{Q}_{1}}}{C}=\dfrac{{{Q}_{2}}}{\left( \dfrac{C}{2} \right)} \\
{} & \Rightarrow {{Q}_{1}}=2{{Q}_{2}}\left( \dfrac{C}{C} \right) \\
{} & \therefore {{Q}_{1}}=2{{Q}_{2}}\ldots \ldots \left( ii \right) \\
   \text{ }\!\!~\!\!\text{ } & {} \\
\end{array}$
From equations $\left( i \right)$ and $\left( ii \right)$,
$\begin{array}{*{35}{l}}
 {} & \left( 2{{Q}_{2}} \right)+{{Q}_{2}}=Q \\
 {} & \Rightarrow 3{{Q}_{2}}=Q \\
 {} & \therefore {{Q}_{2}}=\dfrac{Q}{3}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } \\
\end{array}$
Charge on the capacitor between M and N is ${{Q}_{2}}$
The potential difference between the point M and N is ${{V}_{MN}}=\dfrac{{{Q}_{2}}}{C}$
$\begin{array}{*{35}{l}}
 \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } & {{V}_{MN}}=\dfrac{\left( \dfrac{Q}{3} \right)}{C} \\
 {} & \Rightarrow {{V}_{MN}}=\dfrac{Q}{3C} \\
 \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } & \Rightarrow {{V}_{MN}}=\dfrac{90CV}{3C} \\
 {} & \therefore {{V}_{MN}}=30V\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ } \\
\end{array}$

Hence, the potential difference between M and N is $30V$.

Note: The net potential drop in the right loop which comprises the capacitor $2C,C,2C\text{ and }C$. Total charge gets distributed between right and the left branch because they are connected in parallel. The charges on the capacitors in series are the same.