Question

In series combination of resistances:
(A) p.d. is same across each resistance
(B) total resistance is reduced
(C) current is same in each resistance
(D) all above are true

Answer 1

Hint In order to solve this question, the simple rough diagram is drawn then the rough diagram of series combination of the resistance shows which statement is the correct answer. When the resistance is connected in series there is only one wire used.

Complete step by step solution
Assume that the $p$, $q$ and $r$ are the three resistance which are connected in series.

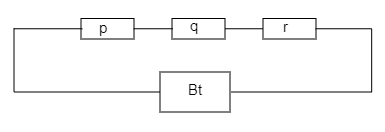
Let assume that the current through the wire is $i$ and the potential difference through the wire is $V$, one end of the wire is connected to the positive terminal of the battery and the other end of the wire is connected in the negative terminal of the battery in between the wire three resistance are connected in series.
If the current crosses the resistance $p$, then the voltage is reduced by $ip$, so the resistance $q$ will get the less voltage than the resistance $p$ and it will again reduce the voltage by $iq$, so the resistance $r$ will get the less voltage than the resistance $q$. So, the potential difference across each resistance is different. The equivalent resistance in series is the sum of all the resistance and it will always be larger than the largest resistance. So, the current flowing the wire is the same through all the three resistance.

Hence, the option (C) is the correct answer.

Note To solve this problem, we have to know that the resistor in series will have the same current and the resistance in series will not have the same voltage. It will be given by the law of the ohm’s law. In ohm’s law, the voltage is directly proportional to the resistance when the resistance is in series.