Question

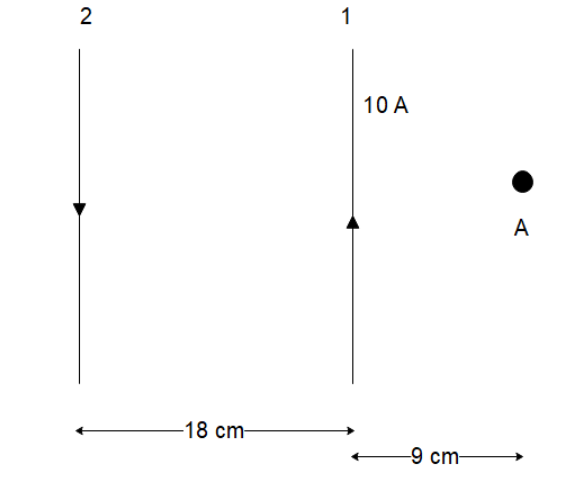
In figure two parallel infinitely long current-carrying wires are shown. If the resultant magnetic field at point A is zero, then determine current ${I_1}$.

A) 50A
B) 15A
C) 30A
D) 25A

Answer 1

Hint: In this solution, we will first determine the magnetic field of the current-carrying cables as a function of the distance of the point from the cable and then we will use the formula to determine the value of the current in the left wire.
Formula used: In this question, we will use the following formula
$B = \dfrac{{{\mu _o}I}}{{2\pi R}}$ where $B$ is the magnetic field generated by an infinite current-carrying wire at a point that is distance $R$ from it.

Complete step by step answer:
The direction of the magnetic field formed by a current-carrying wire can be determined by the right-hand rule. If we place our thumb in the direction of the current, we can determine the direction of the magnetic field as the direction our fingers point in.
For the cable on the left side, the magnetic field will be coming out of the page in the region on the right side of the two cables.
For the cable on the right side, the magnetic field will be going into the page in the region on the right side of the two cables.
So, we can expect the magnetic field in the region on the right side of the two cables to oppose each other.
The distance of the point from the first wire is 9 cm while the distance of the point from the second wire is $18 + 9 = 27\,cm$.
Since the magnetic field at point A is zero, we can say that the two magnetic fields in the opposite direction cancel each other out. So, we can write
$\dfrac{{{\mu _o}{I_1}}}{{2\pi {R_1}}} = \dfrac{{{\mu _o}{I_2}}}{{2\pi {R_2}}}$
Which give us
$\dfrac{{{I_1}}}{{{R_1}}} = \dfrac{{{I_2}}}{{{R_2}}}$
And hence
${I_1} = \dfrac{{{I_2}{R_2}}}{{{R_1}}}$
$ \Rightarrow {I_1} = \dfrac{{27 \times 10}}{3}$
Hence the current in the first cable is

${I_1} = 30\,A$ which corresponds to option (C).

Note: We must be very careful in determining the direction of the magnetic field while using the right-hand rule since the direction of the magnetic field also depends on which side of a cable we are calculating the magnetic field on. While there is no such thing as an infinite cable practically if the point we are measuring the magnetic field is too close to the wire, we can consider the wire to be infinitely long.