Question

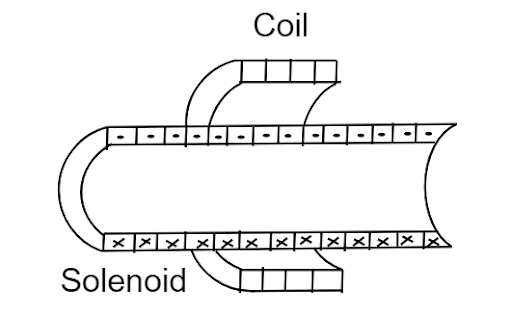
In Figure, a 120- turn coil of radius 1.8 cm and resistance \[5.3\Omega \] is coaxial with a solenoid of 220 turns/cm and diameter of \[3.2cm\]. The solenoid current drops from \[1.5A\]to zero in the time interval \[\Delta t = 25ms\]. What current is induced in the coil during \[\Delta t\]?

Answer 1

Hint:Before we proceed with the problem let’s see what is given. They have given the number of turns in the coil, resistance, solenoid turns, the diameter of the solenoid, and change in current and flux. Using these data first we need to find induced emf using the formula and then by ohm’s law the current can be calculated.

Formula Used:
The formula to find the total induced emf is given by,
\[e = - N\dfrac{{d{\varphi _B}}}{{dt}}\]……… (1)
Where, \[N\] is the number of turns in coil and \[\dfrac{{d{\varphi _B}}}{{dt}}\] is change of magnetic flux wrt to t.

Complete step by step solution:
Consider equation (1)
\[e = - N\dfrac{{d{\varphi _B}}}{{dt}}\]……… (2)
By the definition flux,
\[{\varphi _B} = BA\]
So, substituting the value of value of flux in equation (2) we obtain,
\[e = - N\dfrac{{d\left( {BA} \right)}}{{dt}}\]
Here, we know that, \[B = {\mu _0}ni\] and substitute this value in above equation
\[e = - NA\dfrac{d}{{dt}}\left( {{\mu _0}ni} \right)\]
\[\Rightarrow e = - N{\mu _0}nA\left( {\dfrac{{di}}{{dt}}} \right)\]……… (3)

Then, area of the coil is,
\[A = \pi {r^2}\],
\[\Rightarrow N = 120\],
\[\Rightarrow n = \dfrac{{220turns}}{{cm}}\]
\[ \Rightarrow n = \dfrac{{2200turns}}{m}\]
\[\Rightarrow di = 1.5A - 0 = 1.5A\]
\[\Rightarrow \Delta t = dt = 25 \times {10^{ - 3}}s\]
\[\Rightarrow d = 3.2cm\]\[ \Rightarrow r = 1.6 \times {10^{ - 2}}m\]

Substitute these values in equation (3) we get,
\[e = - 120 \times 4\pi \times {10^{ - 7}} \times 2200 \times \left( {\pi {r^2}} \right)\left( {\dfrac{{1.5}}{{2.5 \times {{10}^{ - 3}}}}} \right)\]
\[\Rightarrow e = - 120 \times 4\pi \times {10^{ - 7}} \times 2200 \times 3.142 \times {\left( {1.6 \times {{10}^{ - 2}}} \right)^2}\left( {\dfrac{{1.5}}{{2.5 \times {{10}^{ - 3}}}}} \right)\]
\[\Rightarrow e = - 0.16V\]

We have found the value of induced emf, now using this find the value of current.By ohm’s law, we know that,
\[i = \dfrac{V}{R}\]
Since V is the potential difference, nothing but emf, so replacing V by e and taking its magnitude, we get,
\[i = \dfrac{{\left| e \right|}}{R}\]
\[\Rightarrow i = \dfrac{{0.16}}{{5.3}}\]
\[\therefore i = 0.031\,A\]

Therefore, the current which is induced in the coil is \[0.031\,A\].

Note:Solenoid depends on the strength of the current, number of turns in the coil and permeability of the material. Its function is to produce a regulated magnetic field through a coil twisted into a compact helix. The solenoid is a sort of electromagnet.