
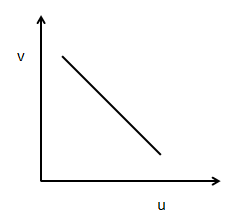
In an experiment to find the focal length of a concave mirror, a graph is drawn between the magnitudes of $u$ and $v$. The graph looks like:
A)
B)
C)
D)

Answer
218.1k+ views
Hint: The image formed is real and inverted when the object is placed in front of a concave mirror and beyond the principal focus of the mirror. In the case of graphs, initially finding the relation between slope, image distance, object distance. to find the nature of the curve.
Complete step by step answer:
The relation between the object distance $u$, the image distance $v$ and the focal length $f$ of the mirror is known as mirror formula. It is given by,
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
It is valid for the both concave and convex mirrors, whether the image formed is real or virtual.
Mirror equation can also be written as,
$ \Rightarrow \dfrac{1}{u} = \dfrac{1}{f} - \dfrac{1}{v}$……………….(1)
Graph is plotted by taking image distance $v$ along y-axis and object distance $u$along x-axis.
Slope of the given graphs is written as,
$ \Rightarrow slope = \dfrac{{Y - scale}}{{X - scale}}$
In the graph the slope can be written as the image distance divided by the object distance.
$ \Rightarrow slope = \dfrac{{dv}}{{du}}$ …………………(2)
Now lets us consider equation (1), and differentiate that equation we get,
Using quotient rule,
$ \Rightarrow \dfrac{d}{{dx}}\left( {\dfrac{u}{v}} \right) = \dfrac{{v.\dfrac{{du}}{{dx}} - u.\dfrac{{dv}}{{dx}}}}{{{v^2}}}$
By doing the simplifications we get,
$ \Rightarrow \dfrac{{vdu - vdv}}{{{v^2}}}$
Apply this formula, we get
$ \Rightarrow \dfrac{{u.d(1) - 1.du}}{{{u^2}}} = \dfrac{{f.d(1) - 1.df}}{{{f^2}}} - \dfrac{{v.d(1) - 1.dv}}{{{v^2}}}$
Differentiation of constants gives us zero.
After solving we get,
$ \Rightarrow \dfrac{{ - 1}}{{{u^2}}}du = 0 - \dfrac{{ - 1}}{{{v^2}}}dv$
Then,
$ \Rightarrow \dfrac{{ - 1}}{{{u^2}}}du = \dfrac{1}{{{v^2}}}dv$
Rearranging the above equation, we get,
$ \Rightarrow \dfrac{{dv}}{{du}} = - \dfrac{{{v^2}}}{{{u^2}}}$ …………………(3)
Now comparing equation (2) and (3) we get
$ \Rightarrow slope = - \dfrac{{{v^2}}}{{{u^2}}}$
$\dfrac{{dv}}{{du}}$ is the slope, that is negative. Therefore, either the curve (C) or the curve (A) is right. Since curves (B) and (D) have a positive slope that cannot be done here.
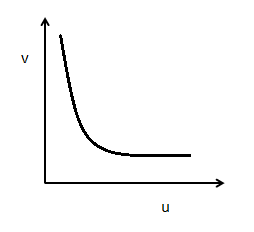
Slope now relies on the $u$ and $v$ values. That is, as per the equation above, it continues to change at any point. So, figure (C) is the correct option.
So, figure (C) is the correct option.
$\therefore $ Correct option is (C).
Note: Focal length of a mirror is the distance between the principal focus and the pole of the mirror. it is denoted by ‘$f$’
Image distance is the distance between the pole of the mirror and image formed. It is denoted by ‘$v$’.
Object distance is the distance between the pole of the mirror and object placed. It is denoted by ‘$u$’.
Complete step by step answer:
The relation between the object distance $u$, the image distance $v$ and the focal length $f$ of the mirror is known as mirror formula. It is given by,
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
It is valid for the both concave and convex mirrors, whether the image formed is real or virtual.
Mirror equation can also be written as,
$ \Rightarrow \dfrac{1}{u} = \dfrac{1}{f} - \dfrac{1}{v}$……………….(1)
Graph is plotted by taking image distance $v$ along y-axis and object distance $u$along x-axis.
Slope of the given graphs is written as,
$ \Rightarrow slope = \dfrac{{Y - scale}}{{X - scale}}$
In the graph the slope can be written as the image distance divided by the object distance.
$ \Rightarrow slope = \dfrac{{dv}}{{du}}$ …………………(2)
Now lets us consider equation (1), and differentiate that equation we get,
Using quotient rule,
$ \Rightarrow \dfrac{d}{{dx}}\left( {\dfrac{u}{v}} \right) = \dfrac{{v.\dfrac{{du}}{{dx}} - u.\dfrac{{dv}}{{dx}}}}{{{v^2}}}$
By doing the simplifications we get,
$ \Rightarrow \dfrac{{vdu - vdv}}{{{v^2}}}$
Apply this formula, we get
$ \Rightarrow \dfrac{{u.d(1) - 1.du}}{{{u^2}}} = \dfrac{{f.d(1) - 1.df}}{{{f^2}}} - \dfrac{{v.d(1) - 1.dv}}{{{v^2}}}$
Differentiation of constants gives us zero.
After solving we get,
$ \Rightarrow \dfrac{{ - 1}}{{{u^2}}}du = 0 - \dfrac{{ - 1}}{{{v^2}}}dv$
Then,
$ \Rightarrow \dfrac{{ - 1}}{{{u^2}}}du = \dfrac{1}{{{v^2}}}dv$
Rearranging the above equation, we get,
$ \Rightarrow \dfrac{{dv}}{{du}} = - \dfrac{{{v^2}}}{{{u^2}}}$ …………………(3)
Now comparing equation (2) and (3) we get
$ \Rightarrow slope = - \dfrac{{{v^2}}}{{{u^2}}}$
$\dfrac{{dv}}{{du}}$ is the slope, that is negative. Therefore, either the curve (C) or the curve (A) is right. Since curves (B) and (D) have a positive slope that cannot be done here.
Slope now relies on the $u$ and $v$ values. That is, as per the equation above, it continues to change at any point. So, figure (C) is the correct option.
So, figure (C) is the correct option.
$\therefore $ Correct option is (C).
Note: Focal length of a mirror is the distance between the principal focus and the pole of the mirror. it is denoted by ‘$f$’
Image distance is the distance between the pole of the mirror and image formed. It is denoted by ‘$v$’.
Object distance is the distance between the pole of the mirror and object placed. It is denoted by ‘$u$’.
Recently Updated Pages
Young’s Double Slit Experiment Derivation Explained

Wheatstone Bridge Explained: Working, Formula & Uses

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




