Question

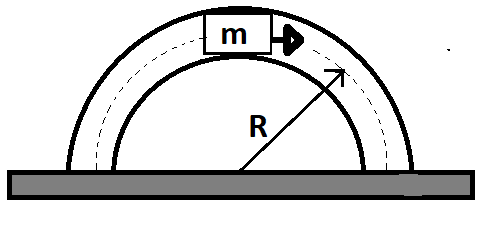
In a vertical plane inside a smooth hollow thin the tube at the block of the same mass as that of the tube is released, as shown in the figure. When it is slightly disturbed it moves towards the right. By the time the block reaches the right end of the tube, the displacement of the tube will be (where R is the mean radius of the tube, assume that the tube remains in the vertical plane)?

Answer 1

Hint:The center of mass is a position defined relative to an object or system of objects. It is the average position of all the parts of the system, weighted according to their masses. For simple rigid objects with uniform density, the center of mass is located at the centroid.
The change in center of mass for a horizontal shift is zero

Complete step by step solution:
From the theory of motion center of mass
We know that for the displacement in the center of mass
\[\Delta {X_{CM}} = \dfrac{{\left( {{M_1} \times \Delta {X_1}} \right) + \left( {{M_2} \times \Delta {X_2}} \right)}}{{{M_1} + {M_2}}}\]
Where,
$\Delta {X_{CM}}$: is the displacement of the center of mass of the system
${M_1}$: is the mass of the tube
${M_2}$ : is the mass of the block
$\Delta {X_1}$ Change in position of the tube
\[\Delta {X_2}\] Change in position of the block
relative position diagram after the displacement has taken place.

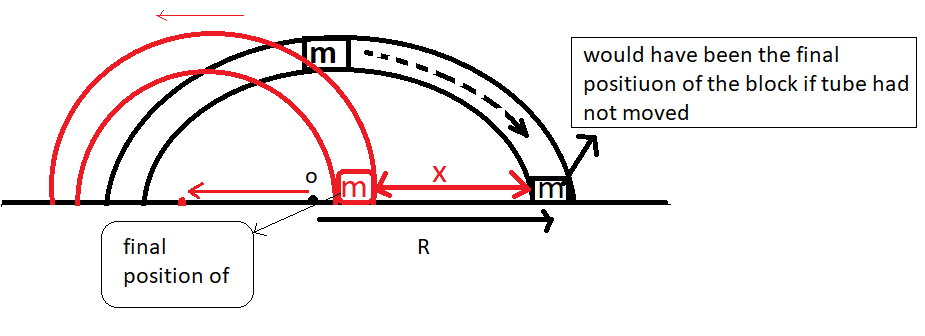
It is a schematic diagram for showing the change in relative positions of the two objects.
Imagine if the tube had not moved and only the block moved then its final position would have been r from the center
Now when the tube had moved x length so it dragged the block with it so now the new position of the block will be x meters away from the point when the tube was fixed and only the block moved.
So the change in position of the the block in two cases will be the difference of two final position (R-x)
and displacement of the the tube will be (x)
Now if the box is moved towards right the the tube will be displaced towards left so new positions of both will be (x) and (R-x)
Now as we know that the change in com for horizontals shift is zero so we can apply displacement formula here
\[\Delta {X_{CM}} = \dfrac{{\left( {{M_1} \times \Delta {X_1}} \right) + \left( {{M_2} \times \Delta {X_2}} \right)}}{{{M_1} + {M_2}}}\]
${M_1}$= m
${M_2}$ = m
$\Delta {X_1}$= x
\[\Delta {X_2}\] = (R-x)
Substituting the values we get
\[
  0 = \dfrac{{\left( {m \times x} \right) + \left( {m \times \left( {R - x} \right)} \right)}}{{m + m}} \\
   \Rightarrow \left( {m \times x} \right) = \left( {m \times \left( {R - x} \right)} \right) \\
   \Rightarrow x = \left( {R - x} \right) \\
   \Rightarrow x = \dfrac{R}{2} \\
    \\
 \]

So the distance traveled by tube will be half of its mean radius.

Note: 1. The Center of mass is an imaginary point where all the mass of a body is concentrated upon.
2. The Center of mass for hollow objects may lie outside the object.
3. The Center of mass of a two-body system is given by:
${X_{cm}} = \dfrac{{{m_1}{x_1} \times {m_2}{x_2}}}{{{m_1} + {m_2}}}$.
4. In a two-body system if the position of the body changes so does its center of mass.
5. If no external force acts on a system of particles, then the center of mass will not move in any direction.