Question

In a cosmic event, suppose a planet heavier than the earth with mass $KM(K > 1)$ and radius $K'R(K' > 1)$ passes through a path near the earth ($M$ and $R$ are the mass and radius of earth). At what closest distance from surface of planet, we are in danger of being thrown into space:

A. ${\left[ {\dfrac{{2KGM}}{g}} \right]^{\dfrac{1}{2}}} - \dfrac{1}{2}K'R$
B. ${\left[ {\dfrac{{KGM}}{{2g}}} \right]^{\dfrac{1}{2}}} - \dfrac{1}{2}K'R$
C. ${\left[ {\dfrac{{KGM}}{g}} \right]^{\dfrac{1}{2}}} - \dfrac{1}{2}K'R$
D. ${\left[ {\dfrac{{KGM}}{g}} \right]^{\dfrac{1}{2}}} - K'R$

Answer 1

Hint: Since the problem is based on gravitational acceleration hence, consider the effect of gravitational force on acceleration due to the gravity of two planets at a distance y from each other. Also, as we all know that the parameters vary with each other hence, analyze every aspect of the solution needed for the question and then present the answer with a proper explanation.

Formula used: The formula of the magnitude of gravitational force due to the Earth is given by:
${F_E} = G\dfrac{{Mm}}{{{R^2}}}$
Here, M is the mass of the earth, R is the radius of the earth and KM is the mass of the heavier planet.

Complete step by step solution:
We know that the magnitude of gravitational force due to the Earth, according to Newton, is given as: -
${F_E} = G\dfrac{{Mm}}{{{R^2}}}$
But also, we have given that KM as mass of the heavier planet and K’R as radius of the heavier planet. Therefore, the magnitude of gravitational force due to the heavier planet will be: -
${F_P} = G\dfrac{{(KM)m}}{{{{(y + K'R)}^2}}}$

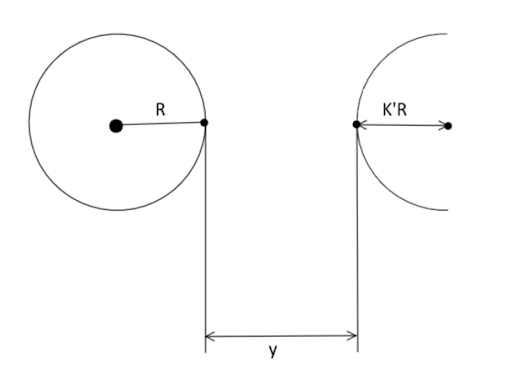
Now, if $y$ is the closest distance as shown in the figure. Then, we will be thrown into space if gravitational force due to the heavier planet will become equal to (or greater than) the weight $mg$ i.e.,
$G\dfrac{{Mm}}{{{R^2}}} = mg \\$
$\Rightarrow G\dfrac{{(KM)m}}{{{{(y + K'R)}^2}}} =mg\\$
$\Rightarrow {(y + K'R)^2} = G\dfrac{{(KM)m}}{{mg}} = \dfrac{{KGM}}{g} \\$
Taking square roots on both sides, we get
$y + K'R = \sqrt {\dfrac{{KGM}}{g}} = {\left( {\dfrac{{KGM}}{g}} \right)^{\dfrac{1}{2}}} \\$
$\therefore y = {\left( {\dfrac{{KGM}}{g}} \right)^{\dfrac{1}{2}}} - K'R \\$
Thus, at a closest distance of ${\left[ {\dfrac{{KGM}}{g}} \right]^{\dfrac{1}{2}}} - K'R$ from the surface of the planet, we are in danger of being thrown into space.

Hence, the correct option is D.

Note: This is a conceptual-based problem hence, it is essential that the given question must be analyzed very carefully to give a precise explanation. While writing a solution, support your explanation by providing proper reasons with the help of formulas and scientific relations and correlate the terms used with each other that might help in the solution.