Question

In a Conical pendulum, a string of length $120cm$ is fixed at rigid support and carries a mass $150g$at the end. If the mass is revolved in a horizontal circle of radius $0.2m$ around a vertical axis, Calculate the tension in the string. $(g = 9.8\dfrac{m}{{{s^2}}})$

Answer 1

Hint: In order to solve this equation, we first have to draw a free body diagram of the body. After that, we have to balance the Net force that is acting on the body. All the forces should be in accordance with Newton's third law. We can easily find the solution after balancing all the forces in all the given directions.

Formula Used:
$Centripetal Force$ = $\dfrac{{m{V^2}}}{r}$
$m$ is the mass of body
$V$ is the velocity of body
$r$ is the radius of circle & Secondly, Net force on a body is equal to $0$ i. e. ${F_{net}} = 0$

Complete step by step answer:
Here, a conical pendulum, a string of length $120cm$ & mass of $150g$ & given we have to calculate the Tension $T$ in the String.
In order to understand the Question, Let’s draw a free body diagram of a pendulum.
Free Body Diagram:

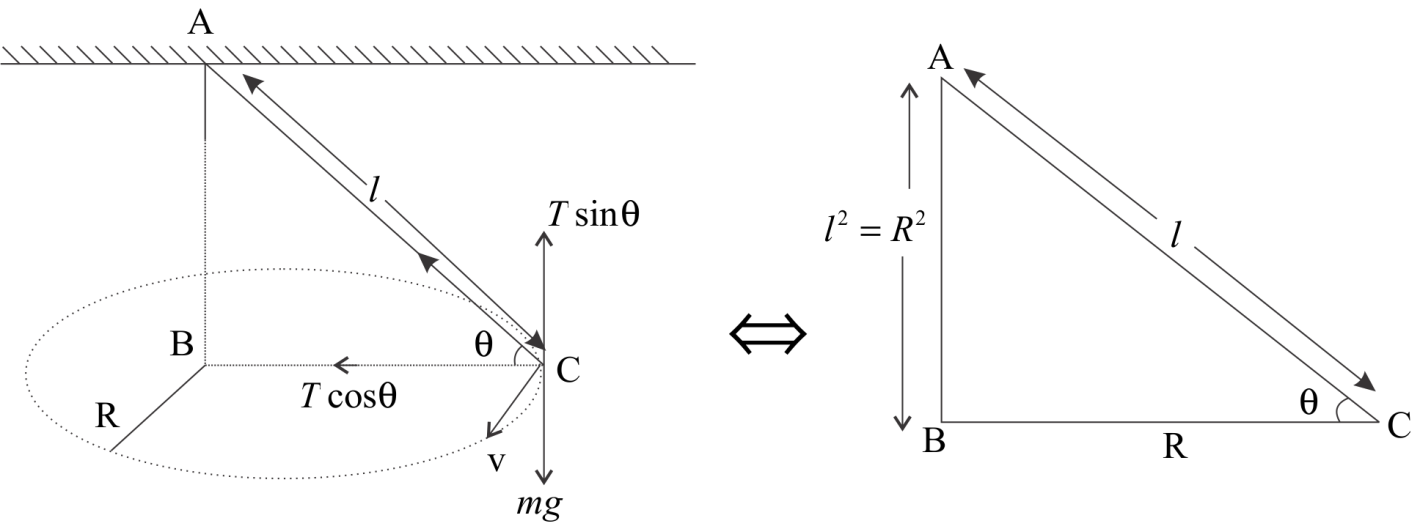
Here the mass $m$ is moving in a circular motion of radius $0.2m$ with velocity $V.$ The Force acting on a mass $m$ will be
${F_{net}} = \dfrac{{m{V^2}}}{r}$
Here, the Tension $T$ will be resolved into two components $T\sin \theta $ (in vertical direction) and $ \uparrow \cos \theta $ (in horizontal direction). Now balancing all forces we get
In Vertical Direction:
$T\sin \theta = mg - (i)$
Now,
In Horizontal plane,
$T\cos \theta = $ Horizontal force on a mass $m$ (i.e. Centripetal force)
So,
$T\cos \theta = \dfrac{{m{V^2}}}{r} - (ii)$
So, from eq. we get
$T = \dfrac{{mg}}{{\sin \theta }}$
Now, In $\Delta ABC$, we get $\sin \theta = \dfrac{P}{H}$
So, $\sin \theta = \dfrac{{\sqrt {{l^2} - {R^2}} }}{l}$
Putting the value of $\sin \theta $in eq. $(1)$ we get
$T = \dfrac{{mgl}}{{\sqrt {{l^2} - {R^2}} }}$
Further,
$T = \left( {\dfrac{{150}}{{1000}}} \right)\dfrac{{(9.8) \times 120}}{{\sqrt {{{(120)}^2} - {{(20)}^2}} }}$ $[1kg = 1000g,1m = 100cm]$
$T = 1.52$ Newton.

Hence, the tension on the string will be $1.52$N.

Note: While solving this question, we have to be very careful with directions. Only forces acting in the same direction will balance each other. Also according to Newton's third law, action and reaction occur on different bodies. So we have to be careful while applying it to anybody. the units for every force should be the same.