Question

If two soaps bubbles of equal radii $r$coalesce, then the radius of curvature of interface between two bubble will be:
A. $r$
B. $0$
C. Infinity
D. $\dfrac{r}{2}$

Answer 1

Hint: The radius of curvature is defined as the approximate circle's radius at a given location. It is equal to the radius of the circular arc that, at that moment, most closely resembles the curve for a curve. As the curve advances, the radius shifts. The radius of curvature, denoted by $R$.

Formula used:
Excess pressure in a soap bubble is calculated using the formula:
$P=\dfrac {4T}{r}$ Where,
r- The radius of the soap bubble
T-The surface tension

Complete answer:
Here, we have given a situation that a radii of the two soaps bubbles are equal, We need to determine the radius of curvature of interface between the two bubble.

Let $R$be the radius of curvature and, $T$ be the surface tensions. In order to know that the radius of curvature is the diameter of a circle that contacts a curve at a particular place and shares its tangent and curvature there.


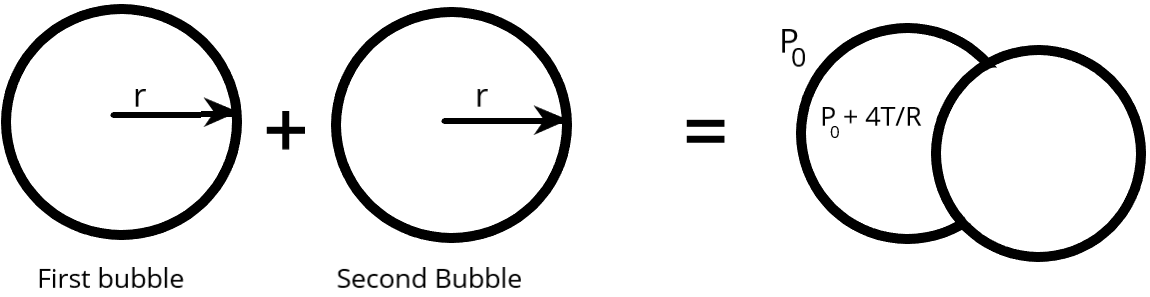
Use the formula of the excess pressure of the bubble $\dfrac{{4T}}{r}$,

From the above figure of the given situation, we have:
The equation of the bubble $1$ is:
${P_0} + \dfrac{{4T}}{r} + \dfrac{{4T}}{r}$.

The equation of the bubble $2$ is:
${P_0} + \dfrac{{4T}}{r}$,

Therefore, At the interface pressure from both sides should be same, then we obtain:
 ${P_0} + \dfrac{{4T}}{r} + \dfrac{{4T}}{r} = {P_0} + \dfrac{{4T}}{r} $
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{r} - \dfrac{1}{r}$
$\Rightarrow \dfrac{1}{R} = 0 $
$\Rightarrow R = \infty $

Thus, the correct option is (C) Infinity.

Note: It should be noted that the excess pressure of the first bubble is two times than the second bubble that’s why the equation of the first bubble is ${P_0} + \dfrac{{4T}}{r} + \dfrac{{4T}}{r}$ instead of ${P_0} + \dfrac{{4T}}{r}$. And when the two bubble soaps' radii aren't equal, air moves from the smaller bubble into the larger one, which causes the larger bubble to expand and the smaller one to diminishes.