Question

If \[\overrightarrow {DA} = \overrightarrow a \] , \[\overrightarrow {AB} = \overrightarrow b \] and \[\overrightarrow {CB} = k\overrightarrow a \] , where, \[k > 0\] and \[X,Y\] are mid-points of \[\overrightarrow {DB} \] and \[\overrightarrow {AC} \] respectively such that \[\left| {\overrightarrow a } \right| = 17\] and \[\left| {\overrightarrow {XY} } \right| = 4\] , then \[k\] is equal to
A. \[\dfrac{8}{{17}}\]
B. \[\dfrac{9}{{17}}\]
C. \[\dfrac{{25}}{{17}}\]
D. \[\dfrac{4}{{17}}\]

Answer 1

Hint: Considering the point D as the origin, the position vectors of all other points A, B, C, X and Y will be found using the given data, Then, the magnitude of the vector \[\left| {\overrightarrow {XY} } \right|\] will be calculated in terms of \[k\] and will be equated to the given numerical value to find the value of \[k\] .

Formulae Used: If \[P,Q\] are two points, \[O\] is the origin and \[\overrightarrow p ,\overrightarrow q \] are the position vectors of \[P,Q\] respectively, then,
1. \[\overrightarrow {PQ} = \] Position vector of \[Q - \] Position vector of \[P\]
\[ \Rightarrow \overrightarrow {PQ} = \overrightarrow q - \overrightarrow p \]
2. The position vector of the midpoint of \[\overrightarrow {PQ} \] is \[\dfrac{1}{2}(\overrightarrow q - \overrightarrow p )\] .


Complete step-by-step solution:
We have been given that \[\overrightarrow {DA} = \overrightarrow a \] , \[\overrightarrow {AB} = \overrightarrow b \] and \[\overrightarrow {CB} = k\overrightarrow a \] .
Let us consider the point \[D\] as the origin and draw a figure with the given vectors as follows:

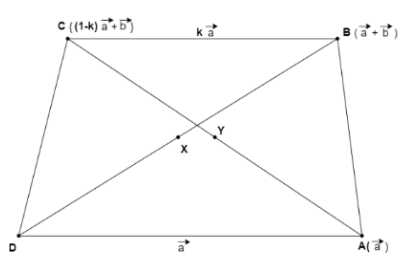
Image: Vector Diagram
Then the position vector of the point \[A = \overrightarrow {DA} = \overrightarrow a \] .
Applying the formula, we have
\[\overrightarrow {AB} = \] Position vector of \[B - \] Position vector of \[A\]
\[ \Rightarrow \overrightarrow b = \] Position vector of \[B - \overrightarrow a \] [Since \[\overrightarrow {AB} = \overrightarrow b \] ]
\[ \Rightarrow \] Position vector of \[B = \overrightarrow b + \overrightarrow a \]
Similarly,
\[\overrightarrow {CB} = \] Position vector of \[B - \] Position vector of \[C\]
\[ \Rightarrow k\overrightarrow a = \] \[(\overrightarrow b + \overrightarrow a ) - \] Position vector of \[C\] [Since \[\overrightarrow {CB} = k\overrightarrow a \] and Position vector of \[B = \overrightarrow b + \overrightarrow a \] ]
\[ \Rightarrow \] Position vector of \[C = \overrightarrow b + \overrightarrow a - k\overrightarrow a \]
\[ \Rightarrow \] Position vector of \[C = \overrightarrow b + (1 - k\overrightarrow {)a} \]
Given that \[X\] and \[Y\] are mid-points of \[\overrightarrow {DB} \] and \[\overrightarrow {AC} \] respectively.
So, the position vector of the point \[X = \dfrac{{\overrightarrow a + \overrightarrow b }}{2}\] [Since \[\overrightarrow {DB} = \overrightarrow b + \overrightarrow a \] ]
And, the position vector of the point \[Y = \dfrac{{(2 - k)\overrightarrow a + \overrightarrow b }}{2}\] [Since \[\overrightarrow {DC} = \overrightarrow b + (1 - k)\overrightarrow a \] and \[\overrightarrow {DA} = \overrightarrow a \]]
Now, \[\overrightarrow {XY} = \] Position vector of \[Y - \] Position vector of \[X\]
\[ \Rightarrow \overrightarrow {XY} = \dfrac{{(2 - k)\overrightarrow a }}{2} - \dfrac{{\overrightarrow b + \overrightarrow a }}{2}\]
\[ \Rightarrow \overrightarrow {XY} = \dfrac{{(1 - k)\overrightarrow a }}{2}\]
We will calculate the magnitude of \[\overrightarrow {XY} \] and equate it to the given numerical values to solve for \[k\]
So, \[\left| {\overrightarrow {XY} } \right| = \dfrac{{(1 - k)}}{2} \times \left| {\overrightarrow a } \right|\]
\[ \Rightarrow 4 = \dfrac{{(1 - k)}}{2} \times 17\] [Since \[\left| {\overrightarrow a } \right| = 17\] and \[\left| {\overrightarrow {XY} } \right| = 4\] ]
\[ \Rightarrow \dfrac{{17(1 - k)}}{2} = 4\]
\[ \Rightarrow 1 - k = 4 \times \dfrac{2}{{17}}\]
Further solving the above
\[1 - k = \dfrac{8}{{17}}\]
\[ \Rightarrow k = 1 - \dfrac{8}{{17}}\]
\[ \Rightarrow k = \dfrac{9}{{17}}\]
Thus, the value of \[k\] is equal to \[\dfrac{9}{{17}}\] .
Hence, option B. is the correct answer.

Note: If \[O\] is the origin, \[A,B\] are two points and \[\overrightarrow a ,\overrightarrow b \] are position vectors of \[A,B\] respectively, then, \[\overrightarrow {AB} = \overrightarrow b - \overrightarrow a \] and \[\overrightarrow {BA} = \overrightarrow a - \overrightarrow b \] . So, \[\overrightarrow {AB} = - \overrightarrow {BA} \] .