Question

If magnification is positive, the nature of the image is:

(A) Real and inverted

(B) Virtual and erect

(C) Real

(D) None of these

Answer 1

Hint Magnification is given by the ratio of image size to the object size $m = \dfrac{I}{O}$ . Cartesian sign conventions say that when the ratio is positive, the image is virtual and erect. When the ratio is negative the image is real and virtual.

Complete step-by-step answer

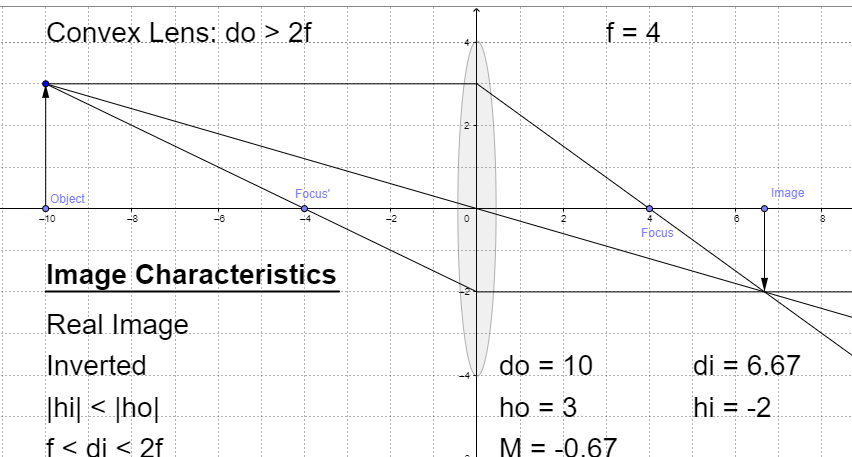
Magnification can be defined as the ratio of size of the image to the size of the object. It is denoted by m.
$m = \dfrac{I}{O}$



For example
This magnification can tell us about the nature of the image based on the sign itself. If the ratio is negative then the image is real and inverted. If the ratio is positive then the image is virtual and erect.

So, according to these sigh conventions, when the magnification is positive then the image has to be erect and virtual.

Hence, the correct option will be B.

Note Lateral magnification is when an object is placed perpendicular to the principle axis.
$m = - \dfrac{v}{u}$

Axial magnification is when object lies on the principle axis
$m = - \dfrac{{{v_2} - {v_1}}}{{{u_2} - {u_1}}}$

Areal magnification is if a 2D object is placed with its plane perpendicular to the principle axis. It is the ratio of area of image to that of object.
$m = \dfrac{{{A_i}}}{{{A_o}}}$ .