Question

If in hydrogen atom, radius of \[{n^{th}}\] Bohr orbits is \[{r_n}\], frequency of revolution of electron in \[{n^{th}}\] orbit is \[{f_n}\], choose the correct option.
A.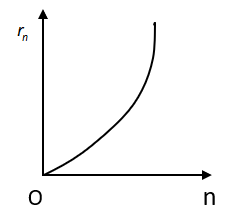
B.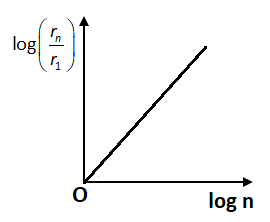
C.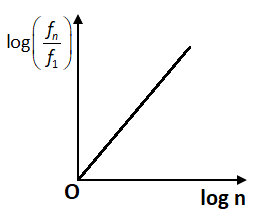
D. Both A and B

Answer 1

Hint:To find the correct graph we need to use the equation for radius of orbit given by Bohr's atomic theory so that we get the relationship between the terms like radius of the orbit, principal quantum number(n), atomic number(Z) and frequency(f).

Formula used:
According to the Bohr's atomic theory,
\[r = \dfrac{{{n^2}{h^2}}}{{4{\pi ^2}m{e^2}}} \times \dfrac{1}{Z}\]
Where n is an integer, \[r\] is the radius of orbit, n is the principal quantum number of the orbit and Z is the atomic number.

Complete step by step solution:
Let us understand each option one by one. As we know from Bohr's atomic theory,
\[{r_n} \propto \dfrac{{{n^2}}}{Z}\]
Here the radius of \[{n^{th}}\] orbit \[{r_n} \propto {n^2}\]. The graph between \[{r_n}\] and n is an increasing parabola. So, in option A, the graph shows the same condition so the first graph is correct.

Also, we can also write \[{r_1} \propto {(1)^2}\] or \[{r_1} \propto {1^2}\]
Now the ratio is given as,
\[\left( {\dfrac{{{r_n}}}{{{r_1}}}} \right) = {\left( {\dfrac{n}{1}} \right)^2 \\ }\]
\[\Rightarrow \log \left( {\dfrac{{{r_n}}}{{{r_1}}}} \right) = 2\log n \\ \]
By comparing this equation with the straight-line equation \[y = mx + c\], we have graph between \[\log \left( {\dfrac{{{r_n}}}{{{r_1}}}} \right)\] and \[\log n\] will be a straight line which is passing from the origin. So, in option B, the graph shows the positive increasing straight line and thus is the correct option.

Similarly, the graph between \[\log \left( {\dfrac{{{f_n}}}{{{f_1}}}} \right)\]and \[\log n\] will be a straight line which is passing from the origin but in a negative slope. In option C, the graph is not representing the negative slope and hence is not the correct answer. Therefore, both the options A and B show the correct graph.

Hence option D is the correct answer.

Note: The Bohr model of an atom came into existence with some modification of Rutherford’s model of an atom. Bohr’s theory modified the atomic structure of the model by explaining that electrons will move in fixed orbitals or shells and each of the orbitals or shells has its fixed energy.