Question

If $\alpha ,\,\beta ,\,\gamma $ be the direction angles of a vector and $\cos \alpha = \dfrac{{14}}{{15}},\,\cos \beta = \dfrac{1}{3}$ then $\cos \gamma = $
A. $ \pm \dfrac{2}{{15}}$
B. $\dfrac{1}{5}$
C. $ \pm \dfrac{1}{{15}}$
D. None of these

Answer 1

Hint: Use the fact that the squares of direction cosines of a vector add up to 1. Direction cosines of a vector whose direction angles are $\alpha ,\,\beta ,\,\gamma $ are $\cos \alpha ,\,\cos \beta ,\,\cos \gamma $. Find $\cos \gamma $ using the formula $\cos \gamma = \pm \sqrt {1 - ({{\cos }^2}\alpha + {{\cos }^2}\beta )} $

Formula used: ${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1$.

Complete step by step solution:
We know that if $\alpha ,\,\beta ,\,\gamma $ are the direction angles of a vector, then $\cos \alpha ,\,\cos \beta ,\,\cos \gamma $ are called direction cosines of that vector.
We also know that the sum of squares of the direction cosines is 1.
Therefore, ${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1$
$\dfrac{{196}}{{225}} + \dfrac{1}{9} + {\cos ^2}\gamma = 1$
${\cos ^2}\gamma = 1 - \dfrac{{221}}{{225}} = \dfrac{4}{{225}}$
$\cos \gamma = \pm \dfrac{2}{{15}}$

Therefore, the correct option is option A. $ \pm \dfrac{2}{{15}}$

Addition information: Direction angles of a vector are the angles between the vector and the x-axis, y-axis and z-axis. Direction cosines are the cosines of the direction angles.

Note: Proof that sum of squares direction cosines is 1.

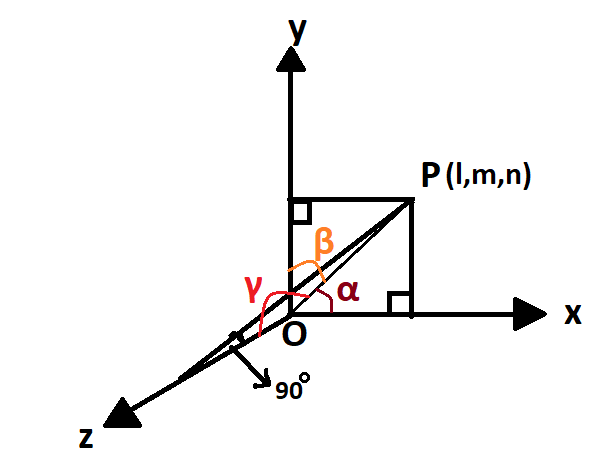
Image: Representation of a point in 3D Coordinate System
Let OP be r. Then $\cos \alpha = \dfrac{l}{r}$, $\cos \beta = \dfrac{m}{r}$ and $\cos \gamma = \dfrac{n}{r}$. We know that ${l^2} + {m^2} + {n^2} = {r^2}$ from the Pythagoras Theorem.
\[{\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = \dfrac{{{l^2}}}{{{r^2}}} + \dfrac{{{m^2}}}{{{r^2}}} + \dfrac{{{n^2}}}{{{r^2}}} = \dfrac{{{r^2}}}{{{r^2}}}\]
Therefore, ${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1$.