Question

If \[a,b,c\] are any three coplanar unit vectors, then:
(A) $a.\left( {b \times c} \right) = 1$
(B) $a.\left( {b \times c} \right) = 3$
(C) \[\left( {a \times b} \right).c = 0\]
(D) $\left( {c \times a} \right).b = 1$

Answer 1

Hint: In order to solve this type of question, first we will make a plane with all the given vectors. Next, we will find out the cross product of two vectors $\overrightarrow b $ and $\overrightarrow c $. Name it as $\overrightarrow d $. Now, we will find out the dot product of the new vector formed i.e., $\overrightarrow d $ with $\overrightarrow a $. Further, we will use the commutative property of vectors to get the desired correct answer.
.
Complete step by step Solution:
We are given three coplanar unit vectors $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $.

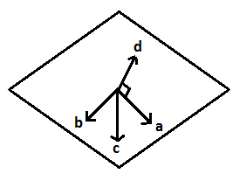
First, we take a plane (as shown in the fig. above) having three vectors $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $.
Cross product of vectors $\overrightarrow b $ and $\overrightarrow c $ will be
$\overrightarrow d = \overrightarrow b \times \overrightarrow c $ ,which is perpendicular to all three vectors i.e., $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $
Now, we will take the dot product of vectors $\overrightarrow a $ and $\overrightarrow d $
$\overrightarrow a .\overrightarrow d = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \theta $
Angle between $\overrightarrow a $ and $\overrightarrow d $ is ${90^ \circ }$
$ \Rightarrow \;\theta = {90^ \circ }$
$\overrightarrow a .\overrightarrow d = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos {90^ \circ }$
$\overrightarrow a .\overrightarrow d = 0$ $\left[ {\because \;\cos {{90}^ \circ } = 0} \right]$
$ \Rightarrow \;\overrightarrow a .\left( {\overrightarrow b \times \overrightarrow c } \right) = 0$
This is called the scalar triple product of $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $.
Further, it can also be written in a cyclic way
\[\overrightarrow a .\left( {\overrightarrow b \times \overrightarrow c } \right) = \overrightarrow c .\left( {\overrightarrow a \times \overrightarrow b } \right) = \overrightarrow b .\left( {\overrightarrow c \times \overrightarrow a } \right)\]
We also know that,
The dot product of vectors is commutative so,
\[\overrightarrow c .\left( {\overrightarrow a \times \overrightarrow b } \right) = \left( {\overrightarrow a \times \overrightarrow b } \right).\overrightarrow c \]

Hence, the correct option is (C).

Note:Whenever we face such questions we should try to first simplify them in terms of $\sin \theta $ and $\cos \theta $ and then solve the rest though this is not a rule and is not compulsory but makes it easier to solve the question. Trigonometric identities should be used carefully as the same identity can be written in different ways at different times.