Question

If a triangle \[ABC\] has vertices \[A\left( { - 1,7} \right)\], \[B\left( { - 7,1} \right)\], and \[C\left( {5, - 5} \right)\]. What is the coordinate orthocentre of the triangle?
A. (-3,3)
B. \[\left( { - \dfrac{3}{5},\dfrac{3}{5}} \right)\]
C. \[\left( {\dfrac{3}{5}, - \dfrac{3}{5}} \right)\]
D. (3,-3)

Answer 1

Hint We will apply the formula of the product of slopes of perpendicular lines to find the equation line perpendicular to \[BC\] and passes through the point \[A\]. Again, we will apply the formula of the product of slopes of perpendicular lines to find the equation line perpendicular to \[AC\] and passes through the point \[B\]. The intersection point of the lines is the orthocentre of triangle \[ABC\].

Formula used
The product of slopes of two perpendicular lines is -1.
The formula for the slope of the line passes through the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is \[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].

Complete step by step solution:

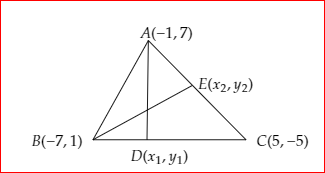
Image: Triangle \[ABC\]

Let \[D\left( {{x_1},{y_1}} \right)\] be a point on \[BC\] and \[AD\] is perpendicular to \[BC\].
Let \[E\left( {{x_2},{y_2}} \right)\] be a point on \[AC\] and \[BE\] is perpendicular to \[AC\].
Now we will find the slopes of \[BC\], \[AD\], \[BE\], and \[AC\].
The slope of the line \[BC\] is \[\dfrac{{ - 5 - 1}}{{5 + 7}} = \dfrac{{ - 6}}{{12}} = - \dfrac{1}{2}\].
The slope of the line \[AD\] is \[\dfrac{{{y_1} - 7}}{{{x_1} + 1}}\].
The slope of the line \[AC\] is \[\dfrac{{ - 5 - 7}}{{5 + 1}} = \dfrac{{ - 12}}{6} = - 2\].
The slope of the line \[AD\] is \[\dfrac{{{y_2} - 1}}{{{x_2} + 7}}\].
Since \[AD\] is perpendicular to \[BC\].
\[\dfrac{{{y_1} - 7}}{{{x_1} + 1}} \cdot \left( { - \dfrac{1}{2}} \right) = - 1\]
\[ \Rightarrow {y_1} - 7 = 2\left( {{x_1} + 1} \right)\]
Replace \[{x_1}\] by \[x\] and \[{y_1}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow y - 7 = 2\left( {x + 1} \right)\]
\[ \Rightarrow y - 7 = 2x + 2\]
\[ \Rightarrow 2x - y + 9 = 0\] ….(i)
Since \[BE\] is perpendicular to \[AC\].
\[\dfrac{{{y_2} - 1}}{{{x_2} + 7}} \cdot \left( { - 2} \right) = - 1\]
\[ \Rightarrow 2\left( {{y_2} - 1} \right) = \left( {{x_2} + 7} \right)\]
Replace \[{x_2}\] by \[x\] and \[{y_2}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow 2\left( {y - 1} \right) = x + 7\]
\[ \Rightarrow 2y - 2 = x + 7\]
\[ \Rightarrow x - 2y + 9 = 0\] ….(ii)
Now multiply 2 with equation (ii) and subtract (i) from it
\[2x - 4y + 18 = 0\]
\[2x - y + 9 = 0\]
\[\overline {\,\,\,\, - 3y + 9 = 0} \]
\[ \Rightarrow 3y = 9\]
\[ \Rightarrow y = 3\]
Substitute \[y = 3\] in equation (i)
\[2x - 3 + 9 = 0\]
\[ \Rightarrow 2x = - 6\]
\[ \Rightarrow x = - 3\]
The coordinate of the orthocentre is \[\left( { - 3,3} \right)\]

Hence option A is the correct option.

Note: An orthocentre is a point that is an intersection point of perpendicular lines which are drawn from a vertex to the opposite side.
Sometimes students take midpoint of \[BC\] to calculate perpendicular line on \[BC\] through the vertex \[A\]. This is an incorrect way. The perpendicular line may not pass through the midpoint. Thus we will assume the coordinate of point \[D\] and \[E\] on the lines \[BC\] and \[AC\] respectively.