Question

If a line makes angles $\alpha ,\beta ,\gamma ,\delta $ with four diagonals of a cube, then what is the value of $\left( {{{\sin }^2}\alpha + {{\sin }^2}\beta + {{\sin }^2}\gamma + {{\sin }^2}\delta } \right)$ ?
A. $2$
B. $\dfrac{4}{3}$
C. $\dfrac{8}{3}$
D. $1$

Answer 1

Hint: Consider a general cube with edges of unit length. Proceed further by calculating the direction ratios of the diagonals. Then, evaluate the values of the cosines of the angles that the line makes with the four diagonals, using the dot product.

Complete step by step Solution:
Imagine a cube with edges of unit length and one vertex on the origin.

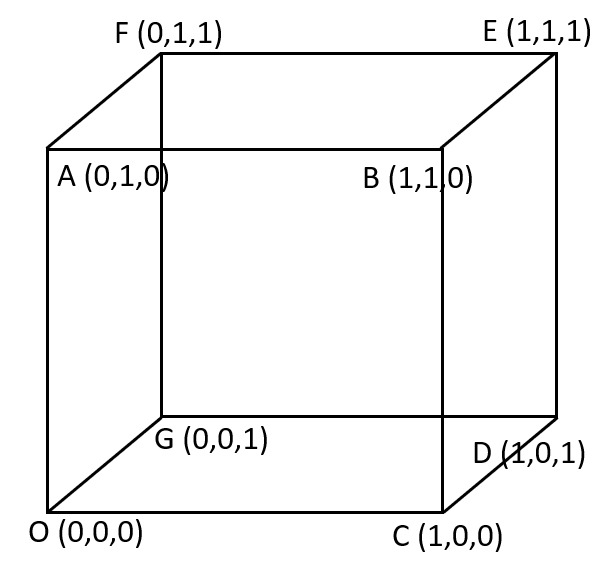
Now, the vector form of these diagonals is:
$\mathop {OE}\limits^ \to = \hat i + \hat j + \hat k$
$\mathop {GB}\limits^ \to = \hat i + \hat j - \hat k$
$\mathop {AD}\limits^ \to = \hat i - \hat j + \hat k$
$\mathop {CF}\limits^ \to = - \hat i + \hat j + \hat k$
The magnitude of all these four diagonals will be the same and it is equal to:
$\sqrt {1 + 1 + 1} = \sqrt 3 $
Thus,
$\left| {\mathop {OE}\limits^ \to } \right| = \left| {\mathop {GB}\limits^ \to } \right| = \left| {\mathop {AD}\limits^ \to } \right| = \left| {\mathop {CF}\limits^ \to } \right| = \sqrt 3 $ … (1)
Now, let the vector form of the line be $l\hat i + m\hat j + n\hat k$ , where $(l,m,n)$ are its direction ratios respectively.
Using the dot product of the line with the diagonals, calculating the cosine of the angles,

Simplifying further and substituting the value from (1),
$\cos \alpha = \dfrac{{l + m + n}}{{\sqrt 3 \sqrt {{l^2} + {m^2} + {n^2}} }}$ … (2)
Similarly,
$\cos \beta = \dfrac{{l + m - n}}{{\sqrt 3 \sqrt {{l^2} + {m^2} + {n^2}} }}$ … (3)
$\cos \gamma = \dfrac{{l - m + n}}{{\sqrt 3 \sqrt {{l^2} + {m^2} + {n^2}} }}$ … (4)
$\cos \delta = \dfrac{{ - l + m + n}}{{\sqrt 3 \sqrt {{l^2} + {m^2} + {n^2}} }}$ … (5)
Squaring and adding equations (2), (3), (4), and (5),
${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma + {\cos ^2}\delta = \dfrac{1}{{3\left( {{l^2} + {m^2} + {n^2}} \right)}}\left[ {{{(l + m + n)}^2} + {{(l + m - n)}^2} + {{(l - m + n)}^2} + {{( - l + m + n)}^2}} \right]$
Expanding the value of the squares and simplifying further by canceling all the terms like $2lm,2\ln ,2mn$ ,
${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma + {\cos ^2}\delta = \dfrac{1}{{3\left( {{l^2} + {m^2} + {n^2}} \right)}}4\left( {{l^2} + {m^2} + {n^2}} \right)$
As ${\cos ^2}\theta = 1 - {\sin ^2}\theta $ , therefore,
$4 - ({\sin ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma + {\sin ^2}\delta ) = \dfrac{4}{3}$
Simplifying further,
${\sin ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma + {\sin ^2}\delta = 4 - \dfrac{4}{3} = \dfrac{8}{3}$

Hence, the correct option is (C).

Note: In this question, it is important to consider a cube in the general form, to obtain the direction ratios of the four diagonals. One would think that using the cross product might be easier as it gives the value in terms of the sine of the angles between the vectors, but it complicates the calculations instead.