Question

If $(a, b)$ is point on the circle whose center is on the $x$-axis and which touches the line $x+y=0$ at $(2,-2)$, then the greatest value of a is
A. $4+2\sqrt{2}$
B. $2+2 \sqrt{2}$
C. $4+\sqrt{2}$
D. None of these

Answer 1

Hint: The slope of a line frequently represents the steepness and orientation of the line. It is easy to determine the slope of a straight line between two points by computing the difference between their coordinates, $(x_1,y_1)$ and. $(x_2,y_2)$

Complete step by step solution:
Consider the figure according to the question

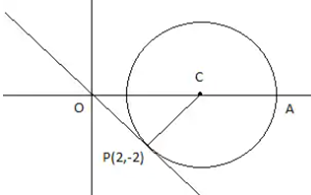
Image: Circle
We know that the equation for slope of a line is
$m=\left(y_{2}-y_{1}\right) /\left(x_{2}-x_{1}\right)$
A line that touches a curve or a circle at one point is said to be tangent. The point of tangency is the intersection of the tangent line and the curve.
The line’s slope is $-1$,
$\therefore \angle {COP}=45^{0}$
$\therefore {OP}=2 \sqrt{2}={CP}$
$\therefore {OC}=\sqrt{(2 \sqrt{2})^{2}+(2 \sqrt{2})^{2}}=4$
The circle's point with the highest ${x}$-coordinate is called ${A}$
$\therefore \text{a}=\text{OA }$
$=\text{OC}+\text{CA}$
$=4+2\sqrt{2}$

Option ‘A’ is correct

Note: The point slope form formula can be used to determine a line's equation. The equation of a line with a given point and a given slope is found using the point slope form. This formula can only be used if the slope of the line and a point on the line are known. The slope-intercept form and the intercept form are two additional formulas that can be used to find the equation of a line.