Question

Helios-B spacecraft had a speed of 71 km/s when it was 4.3 $ \times {10^7}$ km from the sun. What is the shape of its orbit?
A) Circular
B) Helical
C) Elliptical
D) Parabolic

Answer 1

Hint: The shape of the orbit depends on how the speed of the spacecraft at a point compares with the orbital velocity and escape velocity at that point. The mass of the sun is 1.989 $ \times {10^{30}}$ kg.

Complete step by step solution:
The mass of the sun is 1.989 $ \times {10^{30}}$ kg. Let us represent this mass as M. We represent the distance of the spacecraft from the sun as R, which is equal to 4.3 $ \times {10^7}$ km. The velocity of the spacecraft at the given point is v = 71 km/s.
We can find out the shape of the orbit of the spacecraft by comparing its velocity at the given point with the orbital velocity and escape velocity of the spacecraft at that point. Let us see what the shape of the orbit is in different cases:


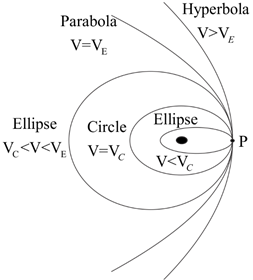
1. If the speed is the same as the orbital velocity, the orbit will be a circle with the center on the central body around which the spacecraft is orbiting.
2. If the speed is less than the orbital velocity, the orbit will be an ellipse smaller than the circle passing through that point and having its center at the central body. The central body will be at the farther focus of the ellipse.
3. If the speed of the spacecraft is more than the orbital velocity but less than the escape speed, then the orbit will be an Ellipse larger than the circular orbit that passes through that point, with the central body at the near focus.
4. If the orbital speed is exactly the escape speed, the orbit will be an open Parabola.
5. If the orbital speed is greater than the escape speed, the orbit will be a Hyperbola. The greater the speed, the "flatter" (more open) the hyperbolic orbit.
So now, we need to find the orbital velocity and escape velocity at the given point, and then compare the velocity of the spacecraft with the obtained velocities.

The expression for orbital velocity is ${v_o} = \sqrt {\dfrac{{GM}}{R}} $, where v$_o$ is the orbital velocity, G is the gravitational constant, M is the mass of the sun, and R is the distance of the spacecraft from the sun.

On substituting the values for all the terms on the right side of the expression for orbital velocity, we obtain the orbital velocity to be equal to,
${v_o} = \sqrt {\dfrac{{\left( {6.67 \times {{10}^{ - 11}}} \right)\left( {1.989 \times {{10}^{30}}} \right)}}{{4.3 \times {{10}^{7 + 3}}}}} = 56 \times {10^3}$ m/s = $56 km/s$
The expression for escape velocity is ${v_e} = \sqrt {\dfrac{{2GM}}{R}} $. We substitute the values of all terms to find the escape velocity, we obtain,
${v_e} = \sqrt {\dfrac{{2\left( {6.67 \times {{10}^{ - 11}}} \right)\left( {1.989 \times {{10}^{30}}} \right)}}{{4.3 \times {{10}^{7 + 3}}}}} = 79.18 \times {10^3}$ m/s = $79.18 km/s$
The velocity of the spacecraft is greater than the orbital velocity but smaller than the escape velocity, so the orbit of the spacecraft is an ellipse greater than the circular orbit.

Therefore, the correct answer for this question is option (C).

Note: The mass of the spacecraft is not required to find out the orbital or escape velocity. These velocities do not depend on the mass of the body which is orbiting the central body.