Question

Find the limit of the perimeter of the regular n polygons inscribed in a circle of radius R as $n \to \infty $ .
A.$2\pi R$
B.$4R$
C.$\pi R$
D.$\pi {R^2}$

Answer 1

Hint: First write the formula of the perimeter of a n sided polygon. Then take the limit as $n \to \infty $and calculate to obtain the required result.

Formula Used:
$1 - \cos 2A = 2{\sin ^2}A$
Length of the side of triangle $c = \sqrt {{a^2} + {b^2} - 2ab\cos \theta } $ , where a and b are the lengths of other sides and $\theta $ is the angle made by the angles of length a and b.

Complete step by step solution:
Suppose a regular polygon with n sides is inscribed in a circle of radius R, with the vertices of the polygon touching the circle.
The diagram of the polygon is,

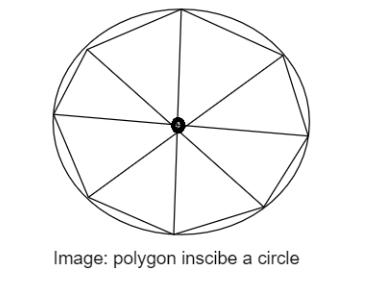
From the center of the circle lines are drawn to each vertex and n triangles are formed.
The lengths of the sides is,
$a = \sqrt {{R^2} + {R^2} - 2.R.R.\cos \dfrac{{2\pi }}{n}} $ , where $\dfrac{{2\pi }}{n}$ is the angle of each triangle at the center.
$ = R\sqrt {2 - 2\cos \dfrac{{2\pi }}{n}} $
$ = R\sqrt 2 \sqrt {2{{\sin }^2}\dfrac{\pi }{n}} $
$ = 2R\sin \dfrac{\pi }{n}$
Therefore, the perimeter is $2nR\sin \dfrac{\pi }{n}$.
As n goes larger the angle $\sin \dfrac{\pi }{n}$approaches $\dfrac{\pi }{n}$ .
Hence the required answer is,
 $2nR \times \dfrac{\pi }{n}$
$ = 2\pi R$

Option ‘A’ is correct

Note: In this question the diagram is important, that will help to clear the concept. Always understand the values of a and b in the length formula, as two sides are the radius of the circle so we put R for a and b then calculated the other one.