Question

Find the domain of \[f\left( x \right)\] if \[f\left( x \right) = {\cos ^{ - 1}}\left( {x - {x^2}} \right) + \sqrt {\left( {1 - \left[ {\dfrac{1}{{\left| x \right|}}} \right]} \right)} + \dfrac{1}{{\left[ {{x^2} - 1} \right]}}\] where \[[.]\] is G.I.F.
A. \[\left[ {\sqrt 2 ,\dfrac{{\left[ {1 - \sqrt 5 } \right]}}{2}} \right]\]
B. \[\left[ {\sqrt 2 ,\dfrac{{\left[ {1 + \sqrt 5 } \right]}}{2}} \right]\]
C. \[\left[ { - \sqrt 2 ,\dfrac{{\left[ {1 \pm \sqrt 5 } \right]}}{2}} \right]\]
D. None of these

Answer 1

Hint: In this question, we have to find the domain of \[f\left( x \right)\] if \[f\left( x \right) = {\cos ^{ - 1}}\left( {x - {x^2}} \right) + \sqrt {\left( {1 - \left[ {\dfrac{1}{{\left| x \right|}}} \right]} \right)} + \dfrac{1}{{\left[ {{x^2} - 1} \right]}}\]. First, we will divide this function in three parts and then will solve them separately and find their domain. Then, we will get three different domains. So, we will find the intersection of all the three domains. That value of intersection will be the final answer.

Formula used:
The domain of basic trigonometric formula and discriminant rule are given as
1. \[{\cos ^{ - 1}}x \in \left[ { - 1,1} \right]\]
2. \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]

Complete step-by-step solution:
Given that \[f\left( x \right) = {\cos ^{ - 1}}\left( {x - {x^2}} \right) + \sqrt {\left( {1 - \left[ {\dfrac{1}{{\left| x \right|}}} \right]} \right)} + \dfrac{1}{{\left[ {{x^2} - 1} \right]}}\]…(1)
Firstly, we will rewrite the equation (1) by making three cases as
\[f\left( x \right) = {f_1}\left( x \right) + {f_2}\left( x \right) + {f_3}\left( x \right)\]…(2)
Now, we will compare equation (1) with equation (2), we get
\[\begin{array}{l}{f_1}\left( x \right) = {\cos ^{ - 1}}\left( {x - {x^2}} \right)\\{f_2}\left( x \right) = \sqrt {\left( {1 - \left[ {\dfrac{1}{{\left| x \right|}}} \right]} \right)} \\{f_3}\left( x \right) = \dfrac{1}{{\left[ {{x^2} - 1} \right]}}\end{array}\].
Further, we will solve the first case that is \[{f_1}\left( x \right) = {\cos ^{ - 1}}\left( {x - {x^2}} \right)\].
As we know, the domain of \[{\cos ^{-1} }x \in \left[ { - 1,1} \right]\]. So, we can write it as
\[ - 1 \le \left( {x - {x^2}} \right) \le 1\]…(3)
Now, we will consider only this part \[ - 1 \le \left( {x - {x^2}} \right)\] from equation (3), we get
\[{x^2} - x - 1 \le 0\]
Further, we will find the roots of the above quadratic equation using discriminant rule where \[a\]is \[1\], \[b\] is \[ - 1\] and \[c\] is \[ - 1\], we get
\[\begin{array}{l}x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\\x = \dfrac{{1 \pm \sqrt {1 - 4\left( 1 \right)\left( { - 1} \right)} }}{{2\left( 1 \right)}}\\x = \dfrac{{1 \pm \sqrt 5 }}{2}\end{array}\]
From above the domain of \[{f_1}\left( x \right)\] we get is
\[\left[ {\dfrac{{1 - \sqrt 5 }}{2} \le x \le \dfrac{{1 + \sqrt 5 }}{2}} \right]\]...(4)
Furthermore, we will solve the second case \[{f_2}\left( x \right) = \sqrt {\left( {1 - \left[ {\dfrac{1}{{\left| x \right|}}} \right]} \right)} \].
As we know, any term in the square root is always greater than zero. So, we get
\[\begin{array}{l}1 - \dfrac{1}{{\left| x \right|}} \ge 0\\1 \ge \dfrac{1}{{\left| x \right|}}\\\left| x \right| \ge 1\end{array}\]
From the above equation the domain we get is
\[x \le - 1,x \ge 1\]…(5)
Now, we will solve the third case \[{f_3}\left( x \right) = \dfrac{1}{{\left[ {{x^2} - 1} \right]}}\].
As we know here \[{x^2}\] can not be equal to \[1\] as if it will be equal to \[1\], then denominator will become \[0\].
So, from above we say that \[{x^2} \ne 1\].
Thus, the domain we get is \[\left[ {{x^2} < 1,{x^2} \ge 2} \right]\]…(6)
Further, we will draw the domain of all three cases on number line as shown below:
The case first:

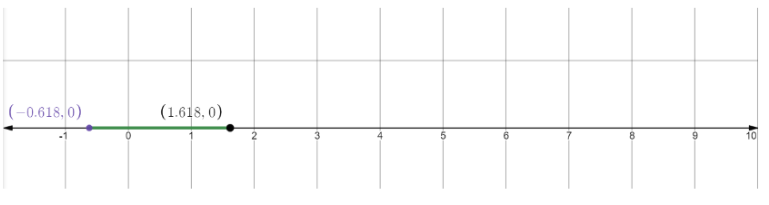
The case second:

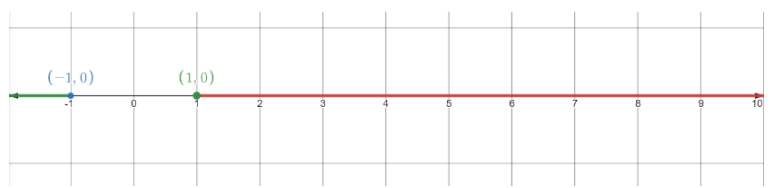
The case third:

Now, we will combine equations (4), (5), (6).
After combining the equation and from the number line we say that the common domain we get for the \[f\left( x \right)\] is \[\left[ {\sqrt 2 ,\dfrac{{\left[ {1 + \sqrt 5 } \right]}}{2}} \right]\]
Hence, the option (B) is correct

Note In this given question, the student should first understand what is being asked in the question and then proceed in the right direction to quickly obtain the correct answer. Furthermore, we should remember the domains and range of the trigonometric and inverse trigonometric functions.