Question

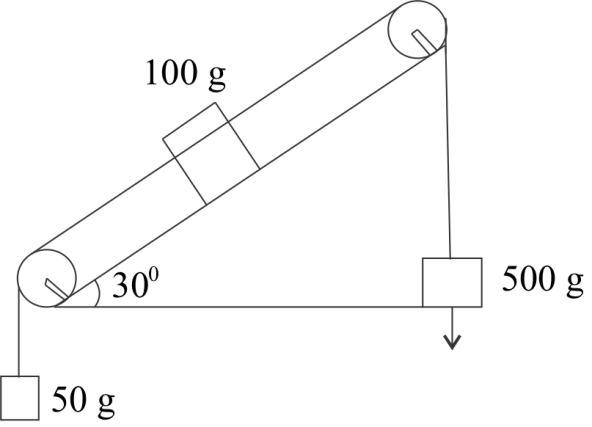
Find the acceleration of ${{500gm}}$ block.

A) $\dfrac{{{{8g}}}}{{{{13}}}}{{downward}}$
B) $\dfrac{{{g}}}{{{{13}}}}{{upward}}$
C) $\dfrac{{{{8g}}}}{{{3}}}{{downward}}$
D) $\dfrac{{{{8g}}}}{{{7}}}{{upward}}$

Answer 1

Hint: In this question, we have a system of three given masses, out of which ${{{M}}_{{1}}}$ is heavy than others which will be pulled downward by gravity and if will further pull the two other masses ${{{m}}_{{1}}}$ and ${{{m}}_{{2}}}$ so by assuming that string is inextensible other masses will move with same acceleration ${{'a'}}$ so by summing up all the forces along with their signs will find acceleration.

Complete step by step solution:
As the block of mass ${{{m}}_{{1}}}$ is suspended with a string it is acted upon by gravity, so force on mass ${{{M}}_{{1}}}$ is.
${{{F}}_{{1}}}{{ = }}{{{M}}_{{1}}}{{g}}{{\_\_\_}}\left( 1 \right)$
As the mass ${{{M}}_{{2}}}$ is lying on an inclined plane of angle of inclination ${{3}}{{{0}}^{{o}}}$, the force acting tangentially downward to the block of mass ${{{M}}_{{2}}}$ is ${{{M}}_{{2}}}{{g sin\theta }}$ as shown in fig. but this is in a direction opposite to the motion of rope so, it will be taken as ${{ - ve}}$ , here we assume that there is no frictional force, so
${{{F}}_{{2}}}{{ = }}{{ - }}{{{M}}_{{2}}}{{g}}{{Sin3}}{{{0}}^{{o}}}\_\_\_\left( 2 \right)$
Further the mass ${{{M}}_{{3}}}$ is pulled upward by the rope so, force which pulled if upward is given by
${{{F}}_{{3}}}{{ = }}{{{M}}_{{3}}}{{g}}$
The net force on the system of three masses is down word i.e. pulls the weight ${{{M}}_{{1}}}$ downward with acceleration ${{a,}}$ so, if ${{M}}$ is net mass of the system i.e. $\left( {{{{M}}_{{1}}}{{ + }}{{{M}}_{{2}}}{{ + }}{{{M}}_{{3}}}} \right){{ = }}{{M,}}$ so net force on the system in given as,
${{F = }}{{Ma}}{{\_\_\_}}\left( 3 \right)$
As we know net force on the system is the sum of all the forces acting on the system i.e.
${{F}}{{ = }}{{{F}}_{{1}}}{{ + }}{{{F}}_{{2}}}{{ + }}{{{F}}_{{3}}}$
Substituting the values of ${{{F}}_{{0}}}{{,}}{{{F}}_{{1}}}{{,}}{{{F}}_{{{2,}}}}{{{F}}_{{3}}}{{,}}$ in above equation we get
${{{M}}_{{a}}}{{ = }}{{{M}}_{{1}}}{{g - }}{{{M}}_{{2}}}{{g}}{{sin3}}{{{0}}^{{o}}}{{ + }}{{{M}}_{{3}}}{{G}}$
$\left( {{{{M}}_{{1}}}{{ + }}{{{M}}_{{2}}}{{ + }}{{{M}}_{{3}}}} \right){{a}}{{ = }}{{g}}\left( {{{{M}}_{{1}}}{{ - }}{{{M}}_{{2}}}{{Sin3}}{{{0}}^{{o}}}{{ + }}{{{M}}_{{3}}}} \right)\_\_\_\left( 4 \right)$
It is given that ${{{M}}_{{1}}}{{ = 500gm}}\,$ or $\dfrac{{{{500}}}}{{{{1000}}}}{{Kg}}$
${{{M}}_{{2}}}{{ = }}{{100gm}}$ or $\dfrac{{{{100}}}}{{{{1000}}}}{{kg}}$
${{{M}}_{{3}}}{{ = }}{{50gm}}$ or $\dfrac{{{{50}}}}{{{{1000}}}}{{ kg }}$ and ${{sin3}}{{{0}}^{{o}}}{{ = }}\dfrac{{{1}}}{{{2}}}$
So, substituting all values in eqn $(4)$ we get
$\dfrac{{\left( {{{50 + 100 + 500}}} \right){{a}}}}{{{{1000}}}}{{ = }}{{g}}\left( {\dfrac{{{{500}}}}{{{{1000}}}}{{ - }}\dfrac{{{{100}}}}{{{{1000}}}}{{ \times }}\dfrac{{{1}}}{{{2}}}{{ + }}\dfrac{{{{50}}}}{{{{1000}}}}} \right)$
$\left( {\dfrac{{{{650}}}}{{{{1000}}}}} \right){{a}}{{ = }}{{g}}\left( {\dfrac{{{{800}}}}{{{{2000}}}}} \right)$
${{65a}}{{ = }}{{g \times 40}}$
${{a}}{{ = }}\dfrac{{{{40g}}}}{{{{65}}}} \Rightarrow {{a}}{{ = }}\dfrac{{{{8g}}}}{{{{13}}}}$

Note: i) If the coefficient of friction is not given n the question then assume that the surface is frictionless
ii) Always consider the string is inextensible in such questions.
iii) It’s always better to draw a free body diagram and depict forces with direction and solve accordingly.